I. Sets in General:
A. Subset: A is a subset of B iff every element of A is also an element of B
B. Equality: A = B iff A is a subset of B and B is a subset of A
C. Power Set : The power set of A is the set whose elements are subsets of A,
i.e.
{B:B is a subset of A}
D. Union: The union of A and B is {x:x is an element of A or x is an element of
B}
E. Intersection: The intersection of A and B is {x:x is an element of A and x is
an
element of B}
F. Difference: The difference of A and B is the set A – B = {x:x is an element
of
A and x is not an element of B}
G. Disjoint: A and B are disjoint iff their intersection is the empty set
H. Complement: If U is the universe and B is a subset of U, then we define the
complement of B to be U – B
I. Union over A: The union over A is {x:x is an element of A for some set A
which is an element of A}
J. Inductive: A set S which is a subset of the set of all natural numbers is
inductive iff for every natural number n, n is element of S implies that n+1 is
an element of S
The PMI/WOP:
II. Definition of the Principle of Mathematical Induction :
A. Definition One:
1. Let P(n) be a statement about a natural number n
2. If:
i. P(1) is true
ii. For every natural number n, P(n) implies P(n+1)
3. Then: For every natural number n, P(n)
B. Definition Two :
1. Let S be a set
2. If:
i. S is a subset of the set of all natural numbers
ii. S is inductive
iii. 1 is an element of S
3. Then: S is the set of all natural numbers
III. Using the PMI:
A. The theorem describes a property that every natural number has
B. So, say, “let P(n) be the statement (the property from the theorem states)”
C. Show that P(1) is true
D. Let nbar be arbitrary
E. Assume P(nbar) and arrive at P(nbar+1)
F. So P(nbar) implies P(nbar+1)
G. So for every n, P(n) implies P(n+1)
H. Since P(1) and for every n, P(n) implies P(n+1), the PMI says, for every n,
P(n)
IV. The Well- Ordering Principle (WOP):
A. If set S is a nonempty subset of the natural numbers, then S has a smallest
element.
B. The WOP is a consequence of the PMI
V. Proving the WOP from the PMI:
A. Assume PMI is true
B. Suppose T is an arbitrary nonempty subset of the natural numbers
C. Let S = the set of natural numbers – T
D. Since T is not empty, S is not equal to the set of natural numbers
E. Suppose T has no smallest element
F. 1 is the smallest natural number, so 1 cannot be in T. So 1 is in S.
G. Suppose n is an element of S
H. No number less than n is in T because one of them would have to be the
smallest element of T
I. n is not an element of T because n is an element of S
J. So n+1 is not an element of T because it would be the smallest member of T.
So n+1 is in S
K. Since 1 is in S and n in S implies n+1 in S, every natural number is in S (by
the PMI)
L. This contradicts the fact that S is not the set of natural numbers
M. So T has a smallest element. So every nonempty subset of the natural numbers
has a smallest element
VI. Using the WOP for Fibonacci number proofs:
A. The proof will be some statement F(n) about Fibonacci numbers
B. Make a set of “Bad” numbers, i.e., natural numbers that do not meet this
property
C. Assume that it is not empty
D. Apply the WOP to get a smallest element b
E. Test by case b = 1 and b = 2. So you know that b is greater than 2.
F. Then you know that anything smaller than b is not is B, so the property is
true
for b - 1 and b – 2, which are both natural numbers. Use this to arrive at a
contradiction.
G. So B is empty
H. So every natural number is not in B
I. So every natural number has property F(n)
Relations:
VII. Relations in General:
A. Ordered Pair : a pair of coordinates , (a.b)
1. Alternate definition: (a,b) = {{a},{a,b}}
B. Equality of Ordered Pairs: (a,b) = (c,d) iff a = c and b = d
C. Cartesian Product: The Cartesian Product of A and B is written as AxB and is
given by AxB = {(a,b):a is an element of A and b is an element of B}
D. Relation: R is a relation from A to B iff R is a subset of AxB
E. R-Related: If (a,b) is an element of R, we write aRb and say that a and b are
R-related
F. Relation on A: A relation R from A to A is called a relation on A
G. Inverse: If R is a relation from A to B, then the inverse of R is R-1 =
{(y,x):(x,y) is an element of R}
H. Composite: If R is a relation from A to B and S is a relation from B to C,
then
the composite of R and S is 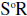 = {(a,c): there
exists an element b of B such
= {(a,c): there
exists an element b of B such
that aRb and bSc}
I. Domain: If R is any relation, then {x: there exists a y such that xRy} is the
domain of R
VIII. Equivalence Relations:
A. Equivalence Relation on A: A relation R is an equivalence relation on A iff R
is reflexive on A, symmetric, and transitive.
B. Reflexive: R is reflexive on A iff for every x in A, xRx
C. Symmetric: R is symmetric iff for every x and y, xRy implies yRx
D. Transitive: R is transitive iff for every x, y, and z, xRy and yRz imply xRz
E. Equivalence Class: Let R be an equivalence relation on A. For x which are in
A, the equivalence class of x determined by R is the set x/R = {y which is an
element of A:xRy}
F. x modulo R: x/R is read as “x modulo R”
G. A modulo R: The set of all equivalence classes is called A modulo R and is
denoted by A/R = {x/R:x is an element of A}
IX. Congruence modulo m:
A. Definition 1: for any natural number m, and for any integers (x,y), x is
congruent modulo m to y iff they have the same remainder when divided by m
B . Definition 2: For any natural number m, and for any integers (x,y), x is
congruent modulo m to y iff m divides x – y.
X. Outline for proving that Definition 1 is equivalent to Definition 2:
A. Use the division algorithm to divide x and y by m
B. Part 1: Assume Definition 1. So set the remainders equal and subtract y from
x . show that m divides x – y.
C. Part 2: Assume Definition 2. So m divides x – y. So x = y + km. Replace y
with its division algorithm form, and then get a second equation for x by
setting it equal to its division algorithm form. Show that the remainders are
equal. (Because DA remainders are unique for each divisor.)
XI. Trick for proving that “(m,n)R(m`,n`) iff mn` = m`n” is transitive: Multiply
the
equation from the first assumed relation by the second coordinate in the third
ordered
pair
Partitions:
XII. Partition: A partition of a nonempty set A is a set A such that:
1. A is a subset of the power set of A
2. Every element of A is not the empty set
3. If X and Y are elements of A, then either X = Y or X and Y are disjoint
4. Every element of A is a member of some element of A
XIII. Outline of proving that for an equivalence relation
R on A, A modulo R is a
partition on A:
A. Let:
1. A be an arbitrary nonempty set
2. R be an arbitrary equivalence relation on A
3. x/R = {y in A:yRx}, for x in A
4. A = A/R = {x/R:x is an element of A}
B. Step One : Prove that A is a subset of the power set of A
1. Make an arbitrary set B, and assume that it is an element of A
2. Pick a b such that B = b/R. So B is not empty because b is in B.
3. Make an arbitrary z and assume it is an element of B
4. So bRz, so (b,z) is an element of R. R is a subset of AxA, so (b,z) is
element of AxA, so z is an element of A.
5. Since z in B implies z in A, B is a subset of A, i.e., B is an element of
the power set of A
6. Since B in A implies B in the power set of A, A is a subset of the
power set of A
C. Step Two : Proving that no element of A is empty
1. Make an arbitrary set B, and assume that it is an element of A
2. Pick a b such that B = b/R. So B is not empty because b is in B.
3. Since B was arbitrary, ever element of A is not empty
D. Step Three: Proving that any two elements of A are either equal or disjoint
1. Make arbitrary sets F and G and assume that they are elements of A.
Assume their intersection is not empty.
2. So then pick a z that is an element of the intersection of F and G
3. Pick f and g such that F = f/R and G = g/R
4. Since z is in both sets, fRz and gRz. Using symmetry and transitivity,
show that fRg and gRf
5. Make an arbitrary s and assume it is an element of F. Show that it is an
element of G.
6. Since s in F implies s in G, F is a subset of G
7. Make an arbitrary s and assume it is an element of G. Show that it is
an element of F.
8. Since s in G implies s in F, G is a subset of F
9. Since F and G are subsets of each other, they are equal.
10. So the intersection of F and G being not empty implies F = G, i.e., the
intersection is empty or they are equal
11. So F and G being in A implies either F and G are equal or disjoint. So
then generalize to all sets F and G
E. Step Four: Proving that every element of A is in some element of A
1. Make an arbitrary x in A
2. So xRx, by reflexivity
3. So x is an element of X = x/R
4. X is an element of A, by definition
5. So x is in an element of A
6. Since x was arbitrary, every x in A is in a member of an element of A
F. Since all four conditions for a partition have been met, A is a partition on
A



