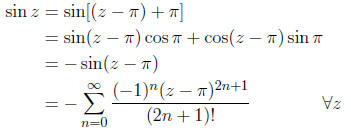Taylor series
The coefficients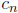 
of the power series
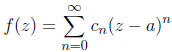
for the function f(z) are given by:
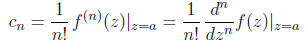
Example:
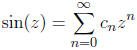
where
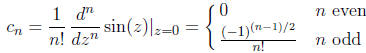
Convergence
If a function has a power series expansion around some point a, then the circle
of convergence
extends to the nearest point at which the function is not analytic. (Analyticity
is a technical
term which you will learn about in PH 461. Brie y, a function which is not
analytic is
singular in some way. A function is certainly not analytic at any point at which
its value
becomes infinite or at a branch point of a root .)
Uniqueness
The power series of a function, if it exits, is unique, i.e. there is at most
one power series of
the form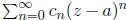 
which converges to a given function
within a circle of convergence
centered at a. We call this a power series " expanded around a".
Note: This theorem is an open invitation to collect a bag of cute tricks. It
doesn't matter
how you find a series for a function, once you have it, it is the series.
The rest of these
theorems should be in your bag of cute tricks.
1. A power series may be differentiated or integrated term
by term. The resulting series con-
verges to the derivative or integral of the function represented by the original
series within
the same circle of convergence as the original series.
Example:
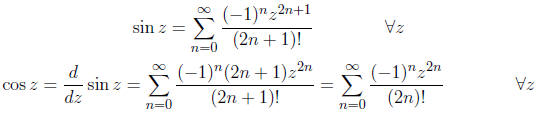
2. One series may be substituted in another provided that
the values of the substituted series
are in the circle of convergence of the other series.
Example:
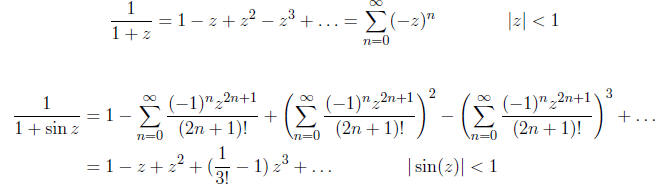
What happens if you try this same trick to find a power
series for 1/(1 + cos z)? Why?
Another example:
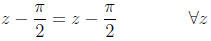
Note: This is a very short power series with just two
non - zero terms .
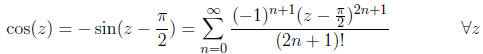
Note: Starting with a power series for sin(z) expanded
around z = 0, we have obtained a
power series for cos(z) expanded around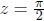 
.
3. Two power series of like powers may be added , subtracted, or multiplied. The
resulting
series converges at least within the common circle of convergence.
Example:
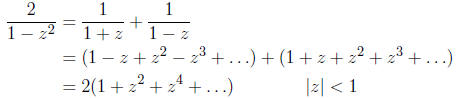
Compare this to the result you would get using the
previous theorem. Which method is
faster?
Another example:
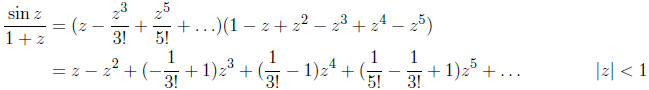
Compare this series to the series for the function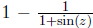
(see
the first example in
Theorem 2.) What can you conclude about the wisdom of assuming two series are
the same
if their first three terms are identical?
4. Two power series expanded around the same point may be divided . If the
leading term(s) of
the denominator series is not zero, or if the zero(s) is canceled by the
numerator , then the
resulting series converges within some circle. If the radius of convergence of
the numerator
and denominator series are 
and
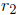, respectively, and the distance from the
origin of the
circles to the nearest zero of the denominator series is s, then the quotient
series converges
at least inside the smallest of the three circles of radii
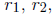, and s.
Try the previous example sin z/(1 + z) using synthetic division , instead. Is
this method
easier or harder? Imagine what you would do if the denominator were a power
series with
an infinite number of non-zero terms.
5. The series expansions for most functions recorded in books are expansions
around the point
z = 0. To expand around a point a ≠ 0 write every z which appears in the
function as
(z - a) + a, simplify creatively , and use Theorem 2.
Example: Expand sin z around z =π .
