Instructions:
• Answer ALL questions from Section A
• You may use a handwritten sheet of notes. Calculators are NOT permitted .
• Read all questions carefully
• Unless explicitly told otherwise, you should explain all your answers fully.
• Do NOT seperate the pages of your exam.
Section A: Answer ALL questions.
Problem A1: [10 pts] (a) Find the slope-intercept equation for the line L
that is perpendicular to 2x−4y−1 = 0
and passes through the point (1, 3).
Solution :
The slope of the line 2x − 4y − 1 = 0 is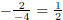 
.
Thus if m is the slope of L then 
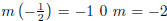. A
point-slope equation for L is then y −3 = −2(x−1). Solving for y , we get the
slope- intercept form y = −2x+5.
(b) Find the equation of the circle for which the line
segment from (1, 3) to (5, 7) is a diameter.
Solution:
The center is the midpoint of line segment which is
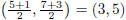. The diameter is the distance between the
endpoints of the segment, i.e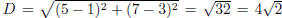 
. The radius r
is then 
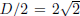. The
equation for the circle is then (x − 3)2 + (y − 5)2 = 8
Problem A2: [10 pts] Let
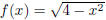and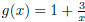 
.
(a) Find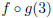 
Solution:
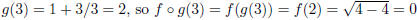
(b) Find the simplest form of
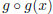that is valid on its
domain.
Solution:
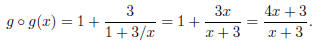
(c) Find the domain of
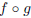. Give your answer in interval
notation.
Solution:
The domain of g is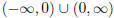 
and the domain of f is [−2, 2]. For x to be
in the domain of 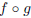we must
therefore have x ≠ 0 and −2 ≤g(x) ≤2. Thus we must solve
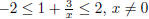. But this implies
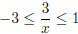
For x > 0, the right inequality implies x/3 ≥1, so x ≥3. For
x < 0 the left inequality implies x/3 ≤−1/3 so
x ≤−1
Problem A3: [10 pts] The graph of y = f(x) is shown below.
On each of the axes below, sketch the required
graph.
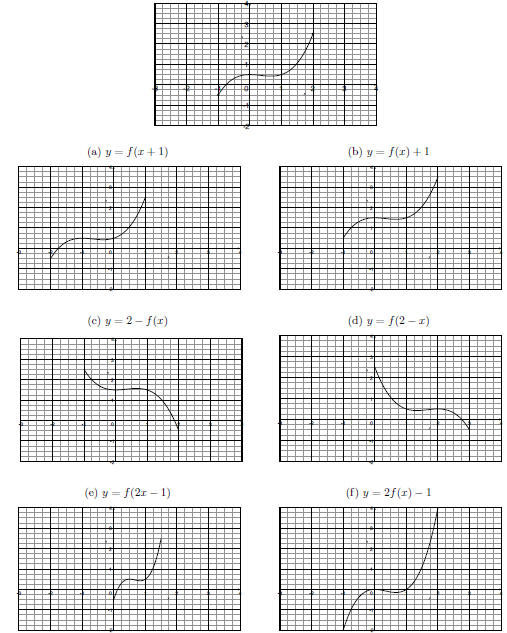
Problem A4: [12 pts] Let
.
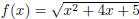(a) If the domain of f is restricted to being the interval[a,∞), what is the
least value of a that ensures f is 1-1?
Solution:
If we complete the square on the quadratic we get x2 + 4x + 5 = (x + 2)2 + 1. We
have only take the right half of
the quadratic so we insist x ≥−2. Since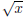 
is
itself 1-1, if we take the domain of f to [−2,∞), we get that f is
1-1.
(b) If f is restricted to the domain from part (a), find
.
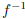Solution:
Set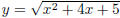 
then y2 = (x + 2)2 + 1 so (x + 2)2 = y2
− 1. Since the domain of f is [−2,∞) we must have
x≥ −2, so we must take the positive square root . Then
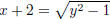and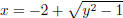 
.
Problem A5: [8 pts] Let P(x) = (x − 2)(x + 1)2
(a) As x → ∞, what happens to P(x)?
Solution:
The leading term is 1x3, so an odd power with positive coefficient
(b) As x → −∞, what happens to P(x)?
Solution:
The leading term is again 1x3, so an odd power with positive coefficient
(c) Sketch the graph of y = P(x) on the axes below
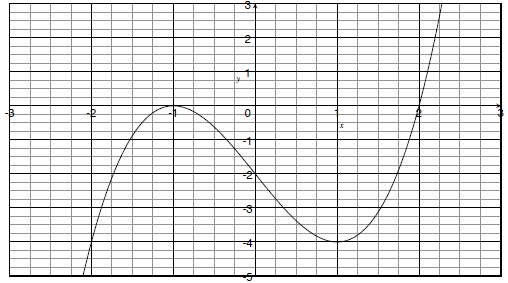
Solution:
The zeros of P (x) are x = 2 and x = −1. Near x = 2, the graph of P(x) looks like
(2+1)2(x−2) = 9(x−2), i.e. a
straight line with slope 9. Near x = −1, the graph of P(x) looks like −3(x +
1)2, so x2 reflected vertically, shifted
1 left and stretched vertically by 3. We plot a couple more points P(0) = −2 and
P(1) − 4 to get a better idea of
the picture.
