Introduction
In general, a set of simultaneous equations link a set of unknown variables
(x,y,x,..) through a set
of equations. In general if there are the same number of variables as there are
equations, then the
equations can be solved to find the variables.
Linear equations with constant coefficients
The most common case of simultaneous equations are those in which the
variables only occur as
themselves, with constant coefficients . For example, consider the following set
of equations
3x + 5y +z = 7
2x - 4y -9z = 36
x - 9y - 2z = 1
With three equations in three variables there will in
general be a solution of these equations.
(Although, see the condition below.)
Solving linear equations with constant coefficients
There a three basic methods which can be used
to solve these equations
• Substitution methods which
progressively reduce the number of
equations by one, until only one
equation in one variable is left. This
allows this variable to be found, and
then by working backwards the
other variables are found. This
method works well when only two
variables and two equations are
involved, but becomes increasingly
tedious as the number of variables
and equations increases.
• By the use of determinants. Again
this is an efficient method when
there are only a few variables and
equations, but as this number
increases so does the number of
determinants to be evaluated, and
the size of the determinants
involved.
• By the use of matrices. This method
is efficient, given an efficient
method for finding the inverse of a matrix.
| Using Maple
The basic command for solving simultaneous
equations using Maple is ‘solve’. It the syntax
>solve({list of equations},{list of variable});
Taking the equations given in the example
these are introduced into Maple as
>eqn1:=3*x + 5*y +z = 7;
>eqn2:=2*x - 4*y -9*z = 36;
>eqn3:=x - 9*y - 2*z = 1;
Maple will then solve these equations using
the command
>solve({eqn1,eqn2,eqn3},{x,y,z});
with the result
{x = 2, y = 1, z = -4} |
Restrictions on solving linear equations with constant
coefficients
If we write the above set of equations in matrix form (AX
= B)
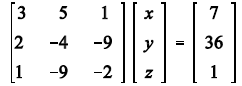
then the solution is X = A-1B. This requires that the
inverse of the matrix A actually exists, which
in turn requires that the determinant of A be non- zero . In this case the
condition is satisfied, direct
calculation shows that det(A) = -258.
However, consider the equations
3x + 5y +z = 7
2x - 4y -9z = 36
8x + 6y - 7z = 1
Defining a matrix A by
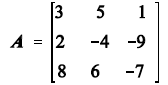
it can be readily shown that det(A) = 0. In this
case there are two possibilities, the equations
are inconsistent (which is actually the case
here) or one of the equations can be derived
from the others and no unique solution exists.
| Maple and unsolvable equations
If you issue the commands
>eqn1:=3*x + 5*y +z = 7;
>eqn2:=2*x - 4*y -9*z = 36;
>eqn3:=8*x +6*y - 7*z = 1;
>solve({eqn1,eqn2,eqn3},{x,y,z});
then Maple will not respond with an answer.
It cannot, the equations are inconsistent, there
is no solution. However modifying eqn3 to
read
>eqn1:=3*x + 5*y +z = 7;
>eqn2:=2*x - 4*y -9*z = 36;
>eqn3:=8*x +6*y - 7*z = 50;
>solve({eqn1,eqn2,eqn3},{x,y,z});
gives the result
{x = -41/29*y+99/29, z = -22/29*y-94/29, y = y}
The equations are not independent, and there
is no unique solution. Maple has chosen to
keep y as a variable, and to solve for x and z
in terms of y . |
Nonlinear equations
Maple can be used to solve nonlinear
equations. As an example, consider the
equations
sin³(x) +sin(y) + z = 9
2cos(x) - 4cos(y) - 9z = 36
sin(x) - 9cos(y) - 2z = 1
Solving these equations by hand is a daunting
task. However, Maple will find a solution to
these equations.
| Maple and nonlinear equations
To get the solution to the equations in the
example, use the commands
>eqn1:=sin(x)^3+sin(y)+z=9;
>eqn2:=2*cos(x) - 4*cos(y) -9*z = 36;
> eqn3:= sin(x) -9*cos(y) - 2*z = 1;
> res:=solve({eqn1,eqn2,eqn3},{x,y,z}):
> evalf(res[1]);evalf(res[2]);evalf(res[3]);
and the result is
x = -2.651396346 + 1.609135585 I
z = -4.881953698 + .3944979774 I
y = -.7192266079 - .4723039785 I
Note - the algebraic output of the ‘solve’
routine has been assigned to the variable array
‘res’, but has been otherwise suppressed by
terminating the line with a colon . Otherwise
the response from Maple is unwieldy. The
next line gives the numerical value of each of
the three elements of the array ‘res’. |



