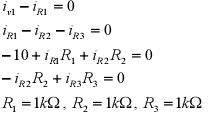Ohms Law
An element with resistance R is called a resistor. Under most conditions,
resistors can be approximate
a linear model . Ohms law relates the voltage and current of resistor, v =i R.
Ohms law can also be
expressed in terms of conductance . The conductance G is the inverse of
resistance. The units of
conductance are Siemens (S). Thus G =1/R and i =G v.
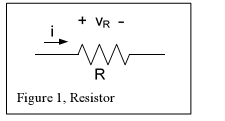
Using Ohms law we can obtain two other forms for the power dissipated by a
resistor.
Nodes and Loops
An electric circuit is one or more circuit elements connected together.
Junctions where two or more circuit
elements are connected together are called nodes. A loop is a closed path that
does not include any node
more than once.
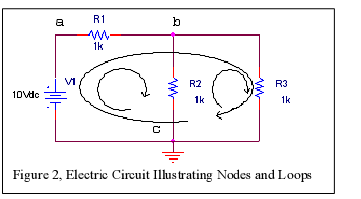
The circuit of Figure 2 has three nodes: a, b, and c and three loops: V1 – R1 –
R2 – V1, V1 – R1 – R3 –
V1, and R2 – R1 – R2.
KCL and KVL
Kirchoff’s current law (KCL): The algebraic sum of the currents entering a node
in a circuit at any instant
in time is zero.
Kirchoff’s voltage law (KVL): The algebraic sum of the voltages around any loop
in a circuit is zero for all
time .
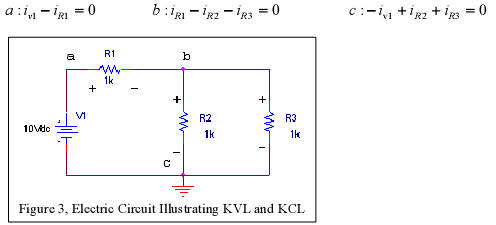
For the circuit of Figure 3, there are three nodes a, b, and c. Writing the KCL
equations for each node we
obtain (assuming currents follow passive convention with exception of current
through source V1 and
negative sign indicates a current leaving the node)
Writing the KVL equations for each node we obtain ( negative sign indicates
voltage drop is from – to +
terminal)
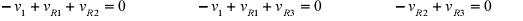
Typically one does not need all possible KCL and KVL equations to solve for
the voltages and currents in
a resistive circuit. One needs enough KCL and KVL equations that when combined
with Ohms law yields
the same number of equations and unknowns.
A system m linear equations in n unknowns can be written in the matrix form Ax =
b, where A is a
m×n matrix of coefficients , x is an n×1 column vector of unknowns, and b is a
m×1 column
vector of constants. The matrix A is square when the number of equations and
unknowns are equal
(m = n) .
When the A matrix is square and has a inverse, then the system of equations has
a unique solution and the
unknowns can be found from x=A-1b
Using Ohms law, some of the KCL and KVL equations, and v1 =10V for the circuit of
Figure 2, we
obtain the following seven equations in seven unknowns
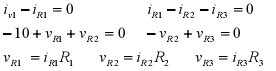
Which we could solve, but substituting the equations from
Ohms law into the KVL equations yields four
equations in four unknowns (the currents) which is simpler to solve . The
voltages can then be found by
substituting the solutions for the currents back into the Ohm’s law equations.