Def: A letter representing an arbitrary number is called a variable.
Def: An algebraic expression is formed by numbers and variables connected by
arithmetic operations.
Ex :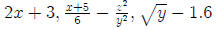 
Def: To evaluate an expression , one substitutes a numeric value for each
variable in an expression .
Ex : When t=5.2,8443t evaluates to 49,903.6
1. Evaluate the area (A=bh) of a parallelogram with base 10 centimeters and 8.2
centimeter height.
2. Evaluate the area (A=(1/2)bh) of a triangle with base and height of 3.5cm and
8cm respectively.
3. Evaluate 3x-y,x=15,y=4
4. Evaluate 2p-q,p=17,q=3
Def : The empty, or null, set is the set of no elements. It is denoted by
either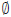 
or {}.
Note : The symbol " ∈" is read "is an element of." Likewise "
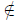" is read "is
not an element of."
Def : The subsets of the real numbers are :
Natural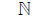
{1,2,3,4...}
Whole 
{0,1,2,3,4,...}
Integers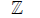
{...,-2,-1,0,1,2,...}
Rational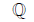
{(p/q):p,q∈
}
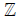Irrational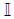 
{
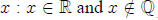} Note:
The symbol is rarely used.
Real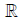 
{x:x has an infinite decimal
expansion}
For a more complete definition of the real numbers, see:
Courant, Richard, and Robbins, Herbert : " What is Mathematics ?"
Chapters 1,2,Oxford, New York (1941)
Complex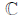 
{z=a+bi,a and b
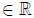,i
is the imaginary unit, i2=-1"}
We will study the complex numbers in detail later on.
Def :The union, denoted ∪, of two sets is the set of all elements of either of
the the individual sets.
Ex :{1,2,3}∪{3,4,5}=
Def :The intersection, denoted ∩ , of two sets is
the set of all elements in each of the individual sets.
Ex :{1,2,3}∩{3,4,5}=
List out the elements in each of the following sets :
5.{x:x∈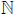
and B is greater than 100}
6.{x:x is a whole number between 0 than 6}
7.{x:x∈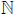 and x is no greater than 20}
Determine wiether each statement is true or false :
8. 3∈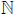
9. 7∈{1,2,3}
Note : A number expressed as a fraction is rational . However, a terminating
or repeating decimal is also
a rational number .
10. 
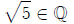
Def : The symbol " ⊆ "denotes a proper subset. That is, every element in the
left hand set is in the
right hand set, and the sets may be equal (having exactly the same elements).
Ex: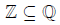 
Def : If the two sets are not equal, one may use the symbol " ⊂ ".
5. Insert the appropriate symbol of those given to make the statement true.
 |
 |
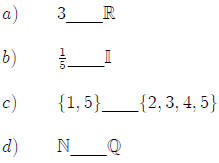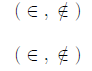(Proper subset or not a proper subset.)
(Proper subset or not a proper subset.) |
Def : The absolute value of a number + is :
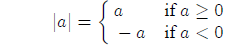
6.Evaluate each absolute value.
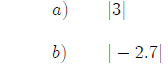
Def : The opposite ( addative inverse ) of a number a is -a.
Def : The reciprocal (multiplicative inverse) of a number a is (1/a).
7. Find the inverses of each number.
Addition
Multiplication
5.4
-3/5
18
-9.6
