1. Refresher on curve types
First, you must know (this should have been in your precalculus course) how
to tell whether a
quadratic equation in two variables is a parabola, ellipse, hyperbola, or one of
their degenerate
forms. (A degenerate parabola is either one line or two parallel lines or the
empty set; a
degenerate ellipse is a point or the empty set; a degenerate hyperbola is a pair
of lines that
intersect.) The simplest forms of the equations are given in the following
table, but with
equations that are more complex , things like completing the square and
substitution of variables
may be necessary to make the equation recognizable. Note in all cases you can
switch x and y
without changing the type of curve given by the equation (e.g. y = x2 and x =
y2 both give
parabolas).
| Common curve equations |
| parabola |
y = ax2 + bx + c, a ≠ 0 |
| ellipse |
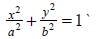 |
| hyperbola |
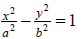 |
| hyperbola |
xy = c , c ≠ 0 |
| degenerate parabola ((parallel)
straight line(s) or empty) |
ax2 + bx + c = 0, a ≠ 0 |
| degenerate ellipse (one point) |
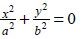 |
| degenerate ellipse (empty set) |
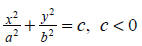 |
| degenerate hyperbola (intersecting
straight lines) |
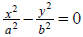 |
| degenerate hyperbola (intersecting
straight lines) |
xy = 0 |
2. Classifying quadric surfaces using traces.
A trace of a surface is what you get by intersecting the surface with a
plane. Usually, when
dealing with traces, we look at planes of the form x = c or y = c or z = c , and
only move on
to other planes if these don’t tell us enough. Most of the time with simple
surfaces, in fact, we
get enough information just by looking at the intersection of the surface with x
= 0 , y = 0 ,
and z = 0 .
Below, we describe the traces usually obtained from our
quadric surfaces (surfaces coming from
quadratic equations in 3 variables), if they’re oriented optimally with respect
to the axes. Note
there is one type of quadratic equation that produces none of the surfaces
listed below – that’s
what happens when a quadratic equation can be written as
(ax + by + cz + d )(ex + fy + gz + h) = 0 , where a, b, c, d, e, f, g and h are
all constants. This
factors as two linear equations, meaning it produces one or two planes (if two
planes, they can be
parallel or intersect). All traces in this case will consist of one or two
straight lines or the entire
plane.
| Surface type |
Surface subtype |
Traces |
| ellipsoid |
|
all traces are ellipses or degenerate ellipses |
| paraboloid |
hyperbolic paraboloid |
parabolas in 2 directions, hyperbolas or
intersecting lines in the third direction. |
| paraboloid |
parabolic cylinder |
parabolas or degenerate parabolas or straight lines
in all 3 directions |
| paraboloid |
elliptic paraboloid |
parabolas in 2 directions, ellipses ( or circles ) in the
third direction |
| hyperboloid |
hyperboloid of two sheets |
hyperbolas (a few degenerate) in two directions,
ellipses in the third direction, and the ellipses in
some cases disappear |
| hyperboloid |
elliptic cone |
hyperbolas (a few degenerate) in two directions,
ellipses in the third direction, and the ellipse for
one trace shrinks to a point but never disappear |
| hyperboloid |
hyperboloid of one sheet |
hyperbolas (a few degenerate) in two directions,
ellipses in the third direction, and the ellipses are
never degenerate (always positive radii ) |
3. Classifying paraboloids using a formula
It turns out that paraboloids are easy to classify. Their equations can
generally be rewritten as
one variable equals a quadratic polynomial in the other two variables. (That
means one variable
starts out only in a linear term .) Suppose z starts out linear, then rewrite the
equation so z
equals a quadratic in x and y. Assume the coefficients are now given by
z = Ax2 + Bxy + Cy2 + Dx + Ey + F
where A, B, C, D, E, and F are constants, and at least one
of A, B, and C is non- zero
(otherwise, we have a plane, not a quadratic).
Then the type of paraboloid is determined by the quantity
B2 - 4AC, which should be
familiar from the quadratic formula. If B2 - 4AC > 0, we have a hyperbolic
paraboloid. If
B2 - 4AC < 0, we have an elliptic paraboloid. If B2 - 4AC = 0, we have a
parabolic
cylinder.
Example: Given the equation 2x + 3x2 -10xz - y + 8z2 =
14z + 9 , we see y is the
variable that only appears in a linear term, so we solve for it in terms of x
and z and rewrite the
equation as y = 3x2 -10xz + 8z2 + 2x -14z - 9 . Now A = 3, B = -10, C = 8, D =
2,
E = -14, and F = -9. Thus B2 - 4AC = 100 - 96 > 0, so this is a hyperbolic
paraboloid.
P.S. If you’re curious, the reason B2 - 4AC arises here
is essentially the same reason it arises
in the quadratic formula – it shows up in the quadratic formula when you
complete the square to
eliminate the linear term, here it shows up if you complete the square to
eliminate the crossproduct
(xy) term.



