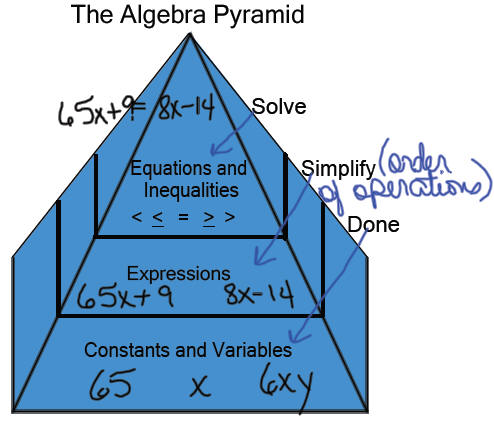
Definitions:
Solution: A number that
makes an
equation true when it replaces the
variable in the equation .
Solution set : A set
containing all the
solutions for a given equation.
Linear equation in one
variable: An
equation with only one variable; the
variable is not raised to a power .
Identity: An equation in
which every real
number (for which the equation is
defined) is a solution.
Contradiction: An
equation that has no
solution.
Addition Principle of
Equality:
If a=b, then a+c=b+c is true for all real numbers a , b, and c.
(If an equation is true and the same number is added to both sides, the equation
is still
true.)
Multiplication Principle of
Equality:
If a=b, then ac=bc is true for all real numbers a, b, and c, where c=0.
(If an equation is true and both sides are multiplied by the same number, the
equation
is still true.)
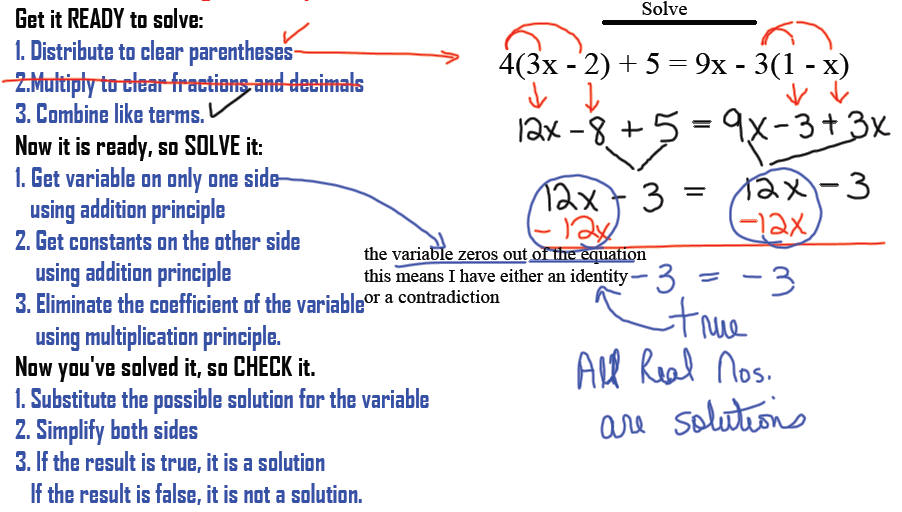
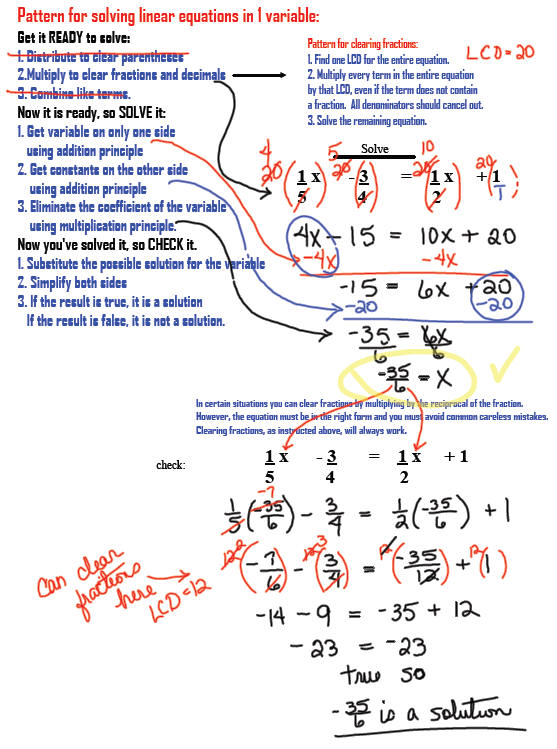
Pattern for solving linear
equations in 1 variable:
Get it READY to solve:
1. Distribute to clear parentheses
2.Multiply to clear fractions and decimals
3. Combine like terms .
Now it is ready, so SOLVE it:
1. Get variable on only one side
using addition principle
2. Get constants on the other side
using addition principle
3. Eliminate the coefficient of the variable
using multiplication principle.
Now you've solved it, so
CHECK it.
1. Substitute the possible solution for the variable
2. Simplify both sides
3. If the result is true, it is a solution
If the result is false, it is not a solution.
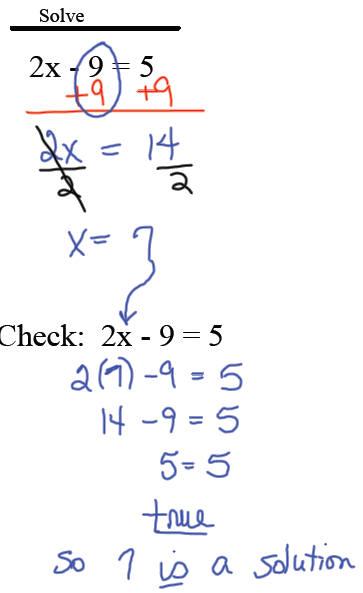
Pattern for solving linear
equations in 1 variable:

Now you've solved it, so CHECK it.
1. Substitute the possible solution for the variable
2. Simplify both sides
3. If the result is true, it is a solution
If the result is false, it is not a solution.
To isolate a particular
variable in a formula:
1. Treat all other variables as constants.
2. Isolate the desired variable using the pattern for solving equations.
Just make up a digit to put in
place of each of
the variables you are NOT solving for... use the
same steps to solve the formula that you would
use to solve the similar equation

