The second midterm examination will be held Monday, 21
November 2005. It will cover
sections 3.7 through 5.1. Here is a list of topics with which you should be
familiar:
• 3.7: Inverse functions: You should understand what it means to be an
inverse function,
understand the conditions under which a function has an inverse, know the round
trip theorem,
know how to find the inverse algebraically , and know how to prove two functions
are inverses
by the round trip theorem. You should also understand the horizontal line test ,
and the
relationship between the graph of a function and its inverse ((x, y) on the
graph of one implies
(y, x) is one the graph of the other, symmetry about the line y = x) . Finally,
you should
know how to restrict the domain of a non-one-to-one function to make it
one-to-one.
• 4.1: Quadratic functions : You should know how to find the vertex of the
graph of a
quadratic function, and how to use this to solve word problems involving
quadratic functions.
• 4.2: Polynomial functions : You should be able to identify the degree,
leading coefficient,
and constant term of a polynomial function. You should be able to perform
polynomial long
division, and be able to state the result (division algorithm) of dividing a
polynomial function
f by a polynomial function h as f(x) = h(x)q(x) + r(x) where r has a lower
degree than
h. You should be able to state and know how to apply the factor and remainder
theorems.
You should know the relationship between a polynomial and the possible number of
roots
and local extrema. Finally, you should understand the properties of the graphs
of polynomial
functions, especially behavior when lxl is large, and how the multiplicity of a
root effects the
corresponding x-intercept.
• 4.5: Rational functions : Given a rational function, you should be able
to determine the
domain, find all holes, vertical asymptotes, y- and x-intercepts, horizontal
asymptotes, all
without a graphing calculator .
• 4.6A: Absolute value inequalities : You should be able to solve absolute
value inequalites
algebraically (NOT using a calculator).
• 5.1: Radicals and rational exponents : You should be able to use the
definition of ab/c
and the exponent laws to simplify expressions involving rational exponents.
Here are some review questions:
1. Finding the inverse algebraically: 3.7: 9-22
2. Round Trip Theorem: §3.7:
23-28. Also, prove that these pairs are inverses using the Round
Trip Theorem:
(a)

(b)
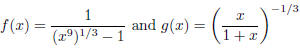
3. Graphs/inverse functions: §3.7:
31-38
4. Domain restriction: §3.7:
39-44
5. Quadratic functions: §4.1:
37-57
6. Leading coefficient , etc. of polys: §4.2:
1-8
7. Polynomial long division: §4.2:
9-14
8. Factor theorem: §4.2:
15-18, 33-59
9. Remainder theorem: §4.2:
23-32
10. Number of roots, local extrema: §4.4:
7-12
11. Multiplicity: §4.2:
43-46.
12. Rational functions: §4.5:
23-40. In addition, for each of the following, find all holes, find
all vertical asymptotes, find all x-intercepts, y-intercepts, and horizontal
asymptotes of the
following rational functions:
(a)
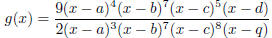
for some real numbers a, b, c, d, and q, none of which are
equal.
(b)
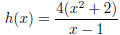
13. Absolute value inequalities: §4.6A:
1-10
14. Radicals and rational exponents: §5.1:
1-10, 23-42
Solutions
You know where to find solutions to odd-numbered book problems. Here are
solutions to the
problems I made up:
• Problem 2a: Note that
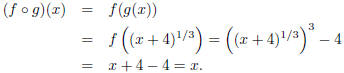
On the other hand,

Thus, by the Round Trip Theorem, f and g are inverse
functions.
• Problem 2b: Note that
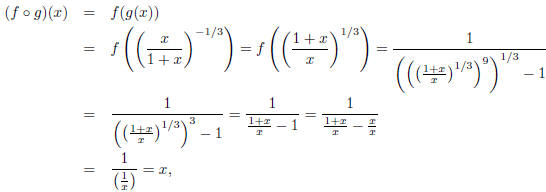
for all x in the domain of g. On the other hand,
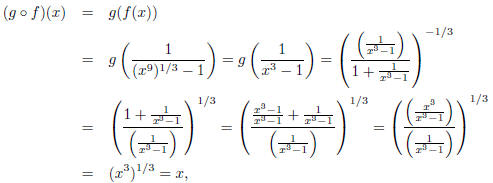
for all x in the domain of f. Thus, by the Round Trip
Theorem, f and g are inverses.
• Problem 12a: We see immediately that we have:
- Domain: All real numbers except x = a, b, c, q.
- Holes: at x = a, b.
- Vertical asymptotes: at x = c, q.
- x-intercepts: x = d.
- y-intercept: (0, 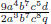 as long a, b, c and q are
not zero .
as long a, b, c and q are
not zero .
- Horizontal asymptote at y = 0.
• Problem 12b: We cannot factor anymore (as x2 + 2 has no roots,
hence no linear factors), so
we have:
- Domain: (-∞, 1), (1,∞)
- Holes: none.
- Vertical asymptotes: at x = 1.
- x-intercepts: none.
- y-intercept: (0,-8)
- Horizontal Asymptote: None.



