The Major Topics of School Algebra

Of course this is just another way of saying that 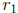and 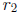are the roots of the quadratic
equation ax² + bx + c = 0.

The preceding discussion reveals that the technique of completing the square is much
more than a skill to solve quadratic equations . Rather, it is the key to the understanding
of quadratic functions in general.

Having quadratic functions available introduces still more word problems to the curriculum,
especially those about falling objects in a gravitational field and certain work
problems which are intractable up to this point. For example: Two workmen , painting at
a constant rate, can paint a house together in 6 days. In how many days can each paint
it alone if it takes one of them 3 days longer than the other to get it done?

The theory of quadratic polynomial functions , as presented above, is nearly complete,
with one small piece missing: what happens when b²−4ac < 0? In the next section, even
this missing piece will be put in place. For polynomial functions in general, there is nothing
as complete and simple. What one can hope to do is to sample a few polynomial functions
of degree > 2, a few others which are not polynomial functions, and then make an effort
to understand two new classes of functions: exponential and logarithmic functions. We
will also make some passing comments on another class of functions that are important
in the sciences: periodic functions. Let us first take up polynomial functions, but with
one caveat that some new information will be withheld until we come to the fundamental
theorem of algebra.

The simplest polynomial functions of higher degrees are those of the form ,
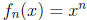where n is a whole number > 1. The similarity in the shapes of the graphs of 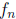to that of
x² for all even n, and to that of x³ for all odd n should be noted. Also noteworthy are the
symmetry properties: for even n, the graph of 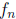has a reflection symmetry with respect
to the y-axis, and for odd n it has a radial symmetry with respect to the origin in the sense
that a point (a, b) is on the graph if and only if (−a,−b) is on the graph. In algebraic
terminology, if n is even, 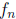is an even function in the sense that 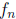(−x) = 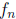(x), and
if n is odd, 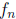is an odd function in the sense that 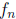(−x) = −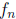(x). Through the
plotting , point by point, of many examples, students can see that the behavior of the
graph of an odd degree polynomial function on the positive x-axis differs from that on
the negative x-axis: one gets higher and higher and the other, lower and lower. The
explanation of this phenomenon in terms of a particular technique of factorization, viz.,

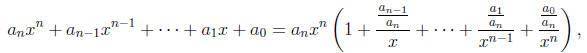
should be taught in place of hand-waving. With the explicit introduction of the intermediate
theorem (without proof, of course), one extracts from this phenomenon the fact
that, although even degree polynomial functions do not always have a zero, the odd degree
ones always do.

The graph of the absolute value function |x|, and the graph of the step function
s(x) so that

s(x) = n for n ≤ x < (n + 1), n an integer

should also be singled out.

Another class of functions whose graphs are interesting are the rational functions ,
i.e., those which are quotients of polynomials, 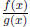, where f(x) and g(x) are polynomials.
Observe that the domain of definition of a rational function is in general not the number
line because of the zeros of the denominator. The simplest among these is the function
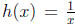. Its graph exhibits a generic phenomenon about rational functions: it has a
horizontal asymptote (x-axis in this case) and a vertical asymptote (y-axis in this case).
More complicated rational functions have slant asymptotes. For example,
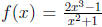
has the line y = 2x for the asymptote. Needless to say, the concept of a limit should
only be introduced informally in this context for the purpose of defining the asymptotes.
Asymptotes are an integral part of the study of rational functions and they add a new
element to the study of algebra.

Before one can tackle exponential functions, one has to discuss with care the concept
of rational exponents. Students should be exposed to the underlying mathematical reason
for the definitions of negative exponents and fractional exponents , which is to be able to
extend the basic laws of exponents

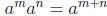and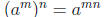

from positive integers m and n to all rational numbers m and n. There is a need to
emphasize the genesis of these definitions, because puzzlement on this subject appears to
be widespread at the moment. Incidentally, before fractional exponents can be defined,
i.e., the fact that 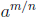is the m-th power of the n -th root of a, a careful discussion of
the existence of the (positive) n-th root is necessary. As in the case of the square root ,
the relevant theorem is that, given a positive number a and a positive integer n, there is
one and only one positive number b so that bⁿ = a. This b is called the (positive) n-th
root of a, to be denoted by 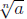. While the existence of 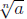must await a thorough study
of the real numbers , students should learn how to prove the uniqueness statement. The
most basic fact governing the operations with n -th roots is 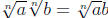, for all positive
a and b, and this too should be proved because the proof introduces students to a typical
bit of abstract thinking. Compare the earlier remark about the square root.

A word of caution is that the same laws for rational exponents, i.e.,

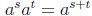and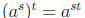

where s and t are now arbitrary rational numbers, are excruciating to prove in general. A
discussion of such laws in school algebra, therefore, would make more sense if it is focused
on a few concrete examples with the intention of making these laws seem reasonable.
Explain that in calculus, all exponents, rational or irrational, will be defined and the laws
of exponents will be proved in one fell swoop rather than piecemeal.

With the availability of the concept of the n-th root of a positive number and the laws
of exponents, one can now introduce radical expressions as numbers created when we
apply to a collection of numbers x, y, etc. not only the existing arithmetic operations on
numbers but also the new operation of taking the r-th power of a positive number, where
r is any rational number. It is only when rational exponents are firmly understood that
radical expressions can be taught as something more than rote procedures. Incidentally,
students should be exposed to the graphs of 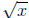(defined only on [0,∞)) and 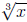(defined
on the x-axis).

Given a positive a, we can now define the exponential function 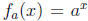. The
number a is the base. A major reason for the introduction of rational exponents is
precisely to make sense of this definition of an exponential function: we now know what
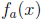is for all rational values of x, and for the purpose of school mathematics, this
knowledge is sufficient (recall FASM). One should emphasize the shape of the graph of
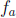: it always passes through (0, 1), but is above the x-axis and rises steeply to the right
if a > 1, and slopes down to the x-axis to the right if a < 1. Contrast this with the graph
of x^a. The number e can be introduced informally at this point in terms of the slope of
the tangent to the graph at (0, 1).

Before introducing logarithms, two things need be done. One is a careful explanation
of the composition of functions, leading to the concept of inverse functions and the
comparison of the graphs of a function and its inverse function. Both concepts are difficult
for students, and the difficulty would likely be exacerbated by the lack of time. This may
be a good reason to cut back on the number of topics in a second-year course in algebra.

The other is the historical reason which led to the discovery of logarithms. It should be
mentioned in an algebra class not only because it is interesting history, but also because
it gives an excellent motivation for the definition of the logarithm.

Let us confine ourselves for the moment only to numbers which can be expressed as
an integer power of 3, i.e.,



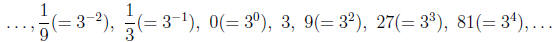
Notice that each such number is identified uniquely with its exponent as a power of 3,
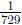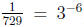i.e., once 3 is fixed, then is uniquely identified with −6 (because ), 81
is uniquely identified with 4 (because 81 = 3⁴), 177147 is uniquely identified with 11
(because 177147 = 3¹¹), etc. Let us devise a notation to indicate this identification: write
L(x) for the exponent of 3 when x is expressed as a power of 3. So



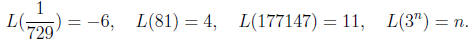
The law of exponents that 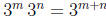is now expressed in the new notation as

L(ab) = L(a) + L(b).

For example,

L(81 × 177147) = L(81) + L(177147)

because



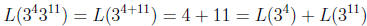
Now suppose we want to find the product of two such numbers, say 177147×243. We
can directly multiply, of course. But four centuries ago, John Napier (1550–1617) made
the observation that, by expressing a number in terms of the exponent of a fixed number
(which is 3 in our case), one could convert multiplication to addition . In greater detail,
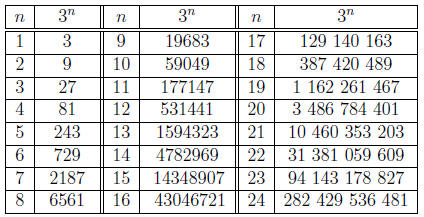
Napier’s observation is the following. His “fixed number” was essentially e, but if he had
used 3 instead of e, he would have had a table of the values of the powers of 3, including
the following:

Then he would be able to use L(177147) and L(243) to do the multiplication of 177147×
243 effortlessly: we have from the table that 177147 = 3¹¹ and 243 = 3⁵, so that



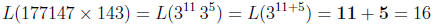
But from the table, we see that L(43046721) = 16. Since as we observed above that
43046721 is the only number identified with 16, we get, for free,

177147 × 143 = 43046721

provided we had the foresight to compile the table. We said we got the result “for free”,
because the only computation we did was to add 11+5. Addition is much simpler than
multiplication.

This discussion would seem to be too restrictive to be of interest. After all, the
integer powers of 3 are a very small collection of numbers. What saves the day is the
fact that every positive real number turns out to be expressible as a power of 3 with a
real exponent. The same principle then shows that if we compile a table of the powers
of 3 for a sufficiently many powers, then we would be able to multiply any two positive
numbers, at least approximately , by use of such a table. In fact, there is no need to
limit the discussion to using 3 as the base; everything that has been said so far holds for
any base. Historically, base 10 was used, and the L in that case is called the common
logarithm, denoted by 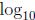. If 3 is used, as is the case at present, then this L would
be written as 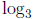. As mentioned above, Napier essentially used e as the base, and loge,
or more simply log in advanced mathematics, is called the natural logarithm. For
over three centuries, tables of logarithms saved scientists countless hours in computations
with data.

With the advent of computer software and calculators , one may legitimately ask what
is the point of learning about the logarithm now? Many reasons, among them the following
two. One is that multiplication is still more complicated than addition, so if a function
log can convert multiplication into addition, in the sense of

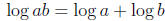for all positive a, b

(i.e., L(ab) = L(a) + L(b)) it is automatically worth knowing. The other reason is that
both exponential functions and logarithms figure prominently not just in mathematics
but in all the sciences. There is no way one can avoid either.