5.2: Students should:
1) Know the two INTERPRETATIONS of probability which dominate the field of
statistics:
(i) Frequentist (objective) interpretation of probability: The probability of a
specific outcome A, P(A), of a
chance experiment is defined as the limiting value of the ratio
 number of times A occurs
number of times A occurs
P(A) = --------------------------------------
 number of times experiment performed
number of times experiment performed
as the number of times the experiment is performed goes to infinity. Note that
P(A) is a constant of nature
whose value is independent of the observer of the experiment and is therefore
objective.
(ii) Bayesian (subjective) interpretation of probability: The probability of
some statement about the nature
of A, P(A), is a measure of the strength of belief that A is true. Since
different individuals will generally
have different degrees of belief concerning the veracity, the value of P(A) will
vary from individual to
individual and is therefore subjective.
2) Know that although the subjective interpretation of probability is, for most
people, the more natural, the
course will use the frequentist interpretation of probability.
3) Know the Probability Axioms, which hold for all interpretations of
probability; see page 199.
4) Know and be able to use the addition rule for disjoint events (pg. 200).
5) Know and be able to use the complement rule (pg. 202).
6) Know and be able to use the general addition rule (pg. 203).
5.3: Student should:
1) Understand conditional probability conceptually.
2) Know definition of conditional probability (page 205).
3) Understand independence conceptually.
4) Be able to determine if two events are independent.
5) Know definition of independence.
6) Know how to compute the probability that at least one of two or more
independent events occurs (page
207-208).
7) Know how to compute the probability that a system consisting of components IN
SERIES and IN
PARALLEL will function.
8) Know the difference between mutually exclusive events and independent events.
5.4: Student should:
1) Know that random variable (RV) is a function that assigns numbers to outcomes
of the sample space.
2) Know definition of DISCRETE and CONTINUOUS random variables (RVs). (page
213).
3) Know now to define events in terms of RVs; see discussion, page 213.
4) Know that distribution functions (density functions and probability mass
functions) are used to assign
probabilities to events involving RVs.
5) Know how to compute probabilities of events involving RVs using distribution
functions and rules from
sections 5.2 and 5.3.
6) Know how to compute the mean, variance, and standard deviation of a random
variable. Note that these
quantities are simply the mean, variance, and standard deviation of the
distribution of the random variable,
respectively; see page 216.
Linear Combination Handout
1) Know definition of independent random variables.
2) Know definition of linear combinations of random variables.
3) Know how to compute mean, variance, and standard deviation of INDEPENDENT
random variables.
4) Know that linear combination of random variables is normally distributed IF
AND ONLY IF those
random variables ARE ALL normally distributed.
5) Know how to use above properties to solve problems involving linear
combinations of RVs.
5.5: Sampling Distributions
1) Understand how a sampling distribution is obtained (for sample mean, sample
median, sample range);
we used the on-line applet on the Rice site to
explore distributions of 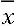
2) Understand that when n is large, the distribution of
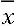 is normal, no matter what the distribution
of the
is normal, no matter what the distribution
of the
original distribution looks like
5.6: Describing Sampling Distributions
1) Determine the distribution of 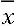 ; discuss
the Central Limit Theorem
; discuss
the Central Limit Theorem
2) Compute probabilities involving 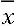
SKIP CHAPTER 6
Chapter 7: Throughout Chapter 7, students must understand that process
data needs to be stationary
before constructing a confidence interval on it.
Note: Teaching chapters 7 and 8 together (e.g., introduce confidence
interval, then hypothesis test or viceversa)
is worth considering and provides a nice connection between CIs and hypothesis
testing.
7.1: (optional per instructor)
7.2: Students should know:
1) How to build a confidence interval for one population mean given a large
sample
2) Interpret a confidence interval (Figure 7.5, pages 297-298)
3) Determine the sample size n given a confidence level, error bound, and sample
standard deviation
Optional: One sided confidence intervals (or confidence bounds)
7.3: Students should know:
1) How to build a confidence interval for a population proportion
NOTE: Do not use book’ s formula , use Wilson estimation, or should we just way
build a confidence
interval for a large sample size???
2) What conditions to check in order to assure that a confidence interval for
the population proportion is
“legal”
3) Be able to determine the sample size n given a confidence level and error
bound, and sometimes
knowing an idea of the true population proportion (for means to estimate π)
4) How to build a confidence interval for the difference of two population means
given large samples; use
ideas of linear combinations to establish the sample mean and sample standard
deviation of 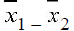
5) How to interpret a confidence interval for the difference of two population
means
Section 8.4 covers checking the normality condition of data; it is suggested
that this section be covered
before 8.1; or actually even before 7.4
7.4: Students should know:
1) How to build a confidence interval for one population mean given a small
sample
2) How to read a t-table
3) How to check for normally distributed data via Ryan-Joiner normality test in
Minitab
4) The conditions to check in order for a t confidence interval to be valid
(normality, population standard
deviations unknown)
5) When to use a z critical value versus a t critical value when constructing a
confidence interval for one
Skip prediction intervals
Skip tolerance intervals
7.5: Students should know:
1) How to build a confidence interval for the difference of two population means
given small samples
assuming unequal population variances ONLY
2) The difference between dependent (paired) and independent two sample data
3) How to build a confidence interval for paired data
4) How to check normality conditions on the difference of paired data
7.6: Students should know:
1) The rationale/process behind building a bootstrap confidence interval
2) How to use Minitab macros (provided by us: bootmean.mac and boot2mean.mac) to
build a bootstrap
confidence interval for one population mean and two population means
Skip other topics in Section 7.6
From Chapter 7, students should know the conditions that must be met to build
the various confidence
intervals, how to check that those conditions are met, and when to use which
confidence interval
construction method
In Chapter 7, students should know how to build these intervals in Minitab, and
check appropriate
conditions in Minitab.
Chapter 8: Throughout Chapter 8, students must understand that process
data needs to be stationary
before constructing a confidence interval on it.
Understand the relationship between confidence intervals and hypothesis testing
Section 8.4 covers checking the normality condition of data; it is suggested
that this section be covered
before 8.1; or actually even before 7.4
8.1: Students should know:
1) Hypothesis testing lingo (null, alternative, Type I Error, Type II Error,
p-values, left/right tailed tests,
reject or fail to reject the null hypothesis, etc.) and how to set up a
hypothesis test (in accordance with this
test, null hypothesis is always =)
2) How to compute Type I Error
3) How to compute Type II Error
4) How to compute a p-value; and how to compare the p-value (observed
significance level ) with α (the
given significance level for the test)
5) When to reject or fail to reject the null hypothesis according to the p-value
and α
6) When to use a right tailed, left tailed, or two-tailed test
8.2: Students should know:
1) How to run a hypothesis test on a single population mean; they need to know
how to check for certain
conditions (stationarity for process data, normality), what is the appropriate
test to run (z, t, bootstrapping),
and how to run it
2) How to run a hypothesis test on the difference of two population means with
independent samples; they
need to know how to check for certain conditions (stationarity for process data,
normality), what is the
appropriate test to run (z, t with unequal variances only, bootstrapping), and
how to run it
3) How to run a hypothesis test on the difference of two population means with
dependent samples; i.e.,
paired data; they need to know how to check for certain conditions (stationarity
for process data,
normality), what is the appropriate test to run (t, bootstrapping), and how to
run it
8.3: Optional
8.4: Students should know:
1) How to determine if sample data is normally distributed via the Ryan-Joiner
test
Skip Chi- squared tests
9.1: Students should know:
1) The basic terminology and concepts (why we are analyzing variance instead of
comparing means,
variance within, variance between, how the test statistic is constructed) of
ANOVA
2) How to determine the degrees of freedom appropriate for using an F table
3) How to read an F table
9.2: Students should know:
1) ANOVA assumptions and how to check if these assumptions are met (via Minitab)
2) How the test statistic is constructed (via SSE, SST, SSTr, etc), though these
values can be obtained from
Minitab output or students should know how to read ANOVA Mintab output to
determine them
3) How to read and fill out an ANOVA table
4) How to set up a hypothesis test for ANOVA
SKIP Chapter 10
11.1: Students should know:
1) The difference between the sample regression line and the population
regression line
2) Estimates of the true population slope and intercept
Skip exponential regression
11.2: Students should know:
1) Properties of the sampling distribution of the sample slope b
2) The basics about how the test statistic for the population slope β is
constructed, and why is makes
sense.
3) How to use Minitab to run a hypothesis test on the population slope β
4) How to construct a confidence interval for β
5) Regression and ANOVA (Optional)



