Suppose that p is a prime number. In a recent article [1]
in this
MAGAZINE, Gregor 
counted the number of 2 × 2 matrices
with entries in the field Z/pZ which have the additional property that
both eigenvalues are also in Z/pZ. In particular, he showed that there
are
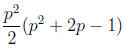
such matrices.
When I began reading 
article, I thought that this would
be an interesting theorem to present to my number theory class. Unfortunately
for me, the key ingredient in his proof is a theorem from
algebra relating the number of elements in a given conjugacy class of
a group to the cardinality of the centralizer of an element in that conjugacy
class. Since many of my students had not yet taken algebra
and would not know about such concepts, I began to look for a proof
which could be taught in an undergraduate number theory class. The
purpose of this note is to provide such a proof.
Our strategy is to use the quadratic formula to find the
roots of the
characteristic polynomial of a matrix and then count the number of
matrices for which these roots are in Z/pZ . We will follow
notation and abbreviate Z/pZ by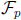 
. Moreover,
all of the variables
and congruences mentioned in the proof should be interpreted modulo
p.
If p = 2, then we cannot divide by 2 and so cannot use the quadratic
formula to find roots of polynomials. However, we can verify by a direct
calculation that of the 16 possible 2 × 2 matrices with entries in
,
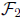the only two whose eigenvalues are not both in
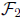are
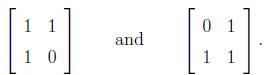
So there are fourteen 2×2 matrices with entries in
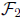and both eigenvalues
in 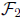, as desired.
If p > 2, then suppose that A is the matrix
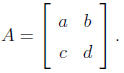
Calculating the characteristic polynomial of A gives us
Char(A) = λ2 − (a + d)λ + (ad − bc).
We want to count the number of choices of a, b, c and d such that
both roots of this polynomial are in
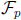. Since p ≠ 2, we can
use the
quadratic formula to find that the roots of Char(A) are
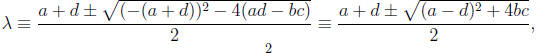
where we interpret dividing by 2 to mean multiplying by
the inverse
and square roots are interpreted modulo p. Clearly, Char(A) has both
roots in 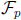if and only if (a − d)2 + 4bc is a perfect square in
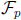. We
will count the number of choices of a, b, c, and d such that this is true.
Let a and d be any fixed elements of
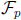. There are p2 choices for
their values. If b 
0, then for each of the p possible choices of c, we
know that
(a − d)2 + 4bc (a − d)2
is a perfect square in 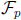. So we have (p2)(1)(p) matrices with entries
in 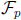, both eigenvalues in
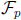and b
0.
If b is one of the p − 1 possible nonzero values, then we use the fact
that including 0 there are precisely (p + 1)/2 perfect squares in
(these being
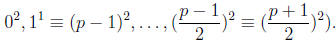
Hence there are (p+1)/2 values that can be added to (a−d)2 to obtain
a perfect square modulo p, and each one of these is a unique multiple of
4b. Thus for each of the p−1 nonzero values of b, we see that there are
(p + 1)/2 values of c such that (a − d)2 + 4bc is a perfect square in
.
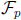So the total number of matrices with entries in
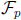, both eigenvalues in
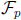, and b
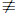0 is (p2)(p − 1)(p + 1)/2. Therefore the total number of
matrices (with any value of b) having entries in
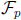and both eigenvalues
in 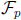is
(
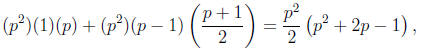
as desired.
