A remarkably elementary proof of the irrationality of e

The standard proofs of the irrationality of e make use of the infinite series representation

or the corresponding alternating series representation for 1/e. (One such proof is given at the end of this
article.) While these proofs are elementary, they obviously require some familiarity with infinite series. The
following proof requires only integration-by-parts and some basic properties of the Riemann integral. The
sum (1) follows as a consequence, thereby making this proof useful as an introduction to infinite series.

e is irrational.

Proof: Suppose e = a/b, where a and b are positive integers . Choose an integer n≥max{b, e}. Now
consider the definite integral 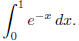This integral is easily evaluated to give 1 − 1/e . On the other hand, repeated integration-by-parts ( n times ) gives

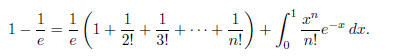
Upon multiplying both sides by e and isolating the integral, we obtain

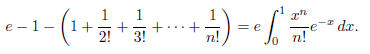
Multiplying both sides of (2) by n! gives

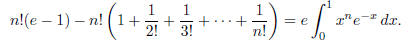
Because of the choice of n and the assumption that e is rational , the left hand side must reduce to an integer .
However the value of the expression on the right is between zero and one. Indeed

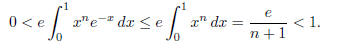
This contradiction implies that e must be irrational.

Notice that the integral in (2) approaches zero as 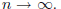Therefore we obtain (1) as a by- product of the
proof . The series representation (1) was derived in a similar way by Chamberland in [1] and by Johnson in
[2].

A proof using the series for 1/e ...

Use the fact that

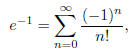
and let S_n denote the nth partial sum of the series:

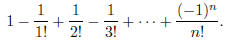
Notice that S_n is a rational number, and it can be written in the form M/n!, where M is an integer. By the
alternating series estimation theorem, it follows that

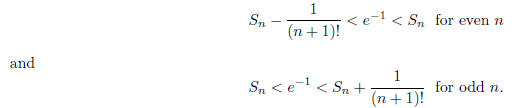
In either case, e⁻¹ is strictly between two rational numbers of the forms 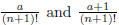, where a is an
integer. It follows that e⁻¹ cannot be written as a fraction with denominator (n + 1)! for any n≥0. Since
any rational number can be written as a fraction with denominator (n+1)!, we conclude that e⁻¹ cannot be
a rational number . Since 1/e is irrational, it follows that e is irrational. (This proof is similar to Sondow’s
geometric proof [3].)