Adding and subtracting radical expressions works like
adding and subtracting expressions
involving variables. Just as we need like terms when combining expressions
involving
variables we need like radicals in order to combine radical expressions.
DEFINITION: Two radicals expressions are said to be
like-radicals if they have the
same indices and the same radicands.
EXAMPLE 1:
a. The expressions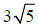 
and
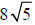are like-radicals.
b. The expressions 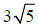and
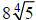are not like radicals since they have
different indices.
c. The expressions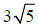 and
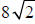are not like radicals since they have
different radicands.
Since only the radicals in a are like, we can only
combine (add and subtract) the radicals in a.
EXAMPLE 2: Add and subtract the pairs of radical
expressions given in EXAMPLE 1 above.
SOLUTIONS : Since only the radicals in a are like, we can only combine
(add or subtract) the
radicals in a.
a. ADDITION:
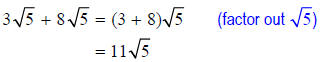
SUBTRACTION:
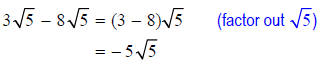
b. Neither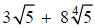 
nor
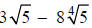can be simplified since the radicals are not
like
( different indices ).
c. Neither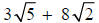 
nor
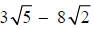can be simplified since the radicals are not
like
(different radicands).
Sometimes we manipulate the involved radicals so that they
are like, and then combine the
expressions .
EXAMPLE: Simplify the following by first obtaining
like-radicals.
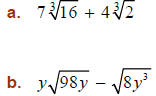
SOLUTIONS:
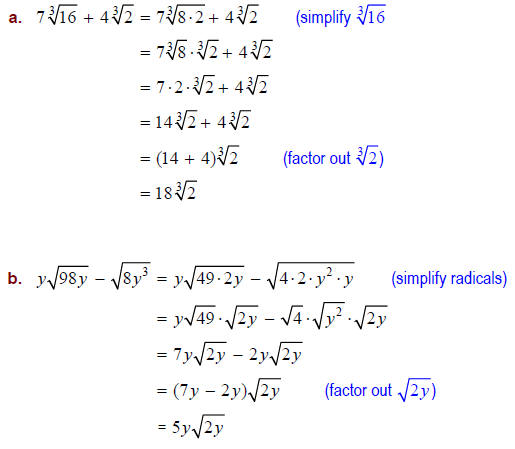
When addition or subtraction is combined with
multiplication, the distributive property is useful.
EXAMPLE: Simplify the following.
SOLUTIONS:
When adding or subtracting is combined with division , we
need to rationalize denominators .
Often, rationalizing a denominator can be accomplished by using a cleaver trick
that involves
the conjugate of the denominator.
DEFINITION: The conjugate of the expression a +b is
the expression a - b.
The conjugate of an expression is a related expression
involving the opposite sign ( +or −).
So the conjugate of express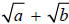ion 
is the
expression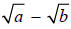 
, while the conjugate of
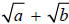is .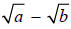
Conjugates are useful when rationalizing denominators since the product of two
conjugates
contains no radicals:
EXAMPLE: Simplify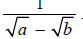 
SOLUTION: If we multiply the denominator by its conjugate,
we will have rationalized the
denominator since the denominator will contain no radicals. In order to avoid
changing the expression , we must also multiply the numerator by the conjugate of
the denominator.
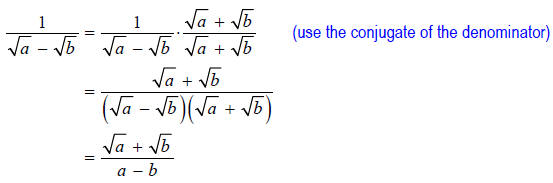
EXAMPLE: Simplify the following.
SOLUTIONS:
Try these yourself and check your answers.
Simplify the following.
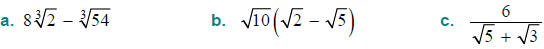
SOLUTIONS:
