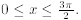Calculus II and Analytic Geometry Study Guide

2 Chapter 6: Applications of definite Integrals

2.1 6.1: Volumes by Slicing and Rotation About an Axis

When: Given a shape defined by a function with independent variable the same as the axis of
rotation.
How: Disk method : .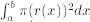
Washer method: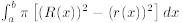
See diagrams in textbook.
Why? Volumes are too difficult to put into regular formulas , so integrals give an exact answer for
almost any function.

2.2 6.2: Volumes by Cylindrical Shells

When: Given a shape defined by a function with independent variable different from the axis of
rotation.
How: Shell method: When rotating about x = L, with height function y = h(x),
Compute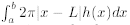
See diagrams in textbook.
Why? The washer method doesn 't always work, especially if the bound function is not well-defined
in terms of the axis of rotation variable.

2.3 6.3: Lengths of Plane Curves

When: Given a path defined parametrically or as a function and asked for its length based on
bounds of parameters.
How: Shell method: When rotating about x = L, with height function y = h(x),
Compute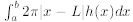
See diagrams in textbook.
Why? The washer method doesn 't always work, especially if the bound function is not well-defined
in terms of the axis of rotation variable.

2.4 6.4: Areas of Surfaces of Revolution

When: Given a surface in three dimensions, calculate the area by integration.
How: For a curve y = f(x) over x ∈ [a, b] revolving around the x-axis, evaluate

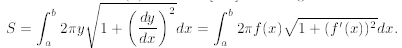
For a curve x = g(y) over y ∈ [a, b] revolving around the y-axis, evaluate

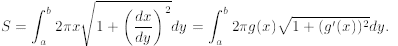
For a parametric curve x = f(t), y = g(t) for a ≤t ≤b revolved around y-axis, evaluate

For a parametric curve x = f(t), y = g(t) for a ≤ t ≤b revolved around x-axis, evaluate

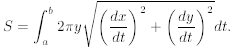
Why? Not all surfaces have nice formulas , so integrals are needed.
 

3 Problems

(*) denotes a difficult problem.

Evaluate:

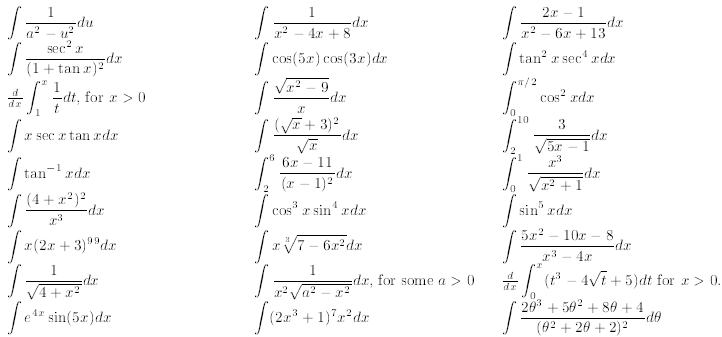
State whether the integral converges or diverges. If it converges, evaluate.

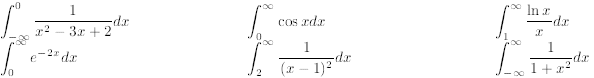
For the following integrals, find the minimal number of intervals required for (a) the Trapezoidal rule, and (b)
Simpson' s rule . Then, compute the minimum error guaranteed when n = 100.

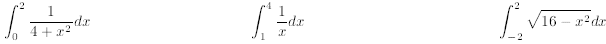
Consider the following problems:

Compute the area between the x-axis and the
curve f(x) = 4 - 2 sin² x.

Find the area between the curves y = e^-x and
y = x² where 1 ≤x ≤4.

*Find the volume of a "donut." Let
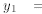
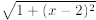be the top of the circle of ra -
dius 1 around the point (2, 0) and let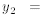
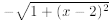be the bottom of the same cir-
cle. Let the region between 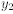and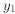 be revolved
around the y-axis. Compute the volume.

Find the general form for y if 
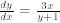
If 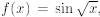, find the area of the region be-
tween the x-axis and f(x) from 0 to π⁴.

A spherical tank of radius 10 feet is filled with
water. Find the work done in pumping all of the
water out through the top of the tank. Recall that
the density of water is ≈ 62.4lb/ft³.

A cup of fast food coffee is 180 °F when freshly
poured. After 2 minutes in a room at 70 °F, the
coffee has coooled to 165 °F. Find the temperature
at any time t and find the time at which the coffee
has cooled to 120 °F.

Does the integral 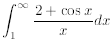converge or di-
verge?

Suppose the line segment 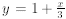from x = 0 to
x = 12 is revolved about the x-axis. The resulting
solid looks like a megaphone . Compute the volume
of this solid.

*Construct a volume by rectangular cross-sections
for 0 ≤ x ≤1: the base extends from y = 0 to
y = 1 - x³, and the height is x².

Let R be the region bounded by y = 4 - x² and
y = 0. Find the volume of the solids obtained by
revolving R about each of the following: (a) the
y-axis, (b) the line y = -3, and (c) the line y = 7.

*Find the volume of the solid given by rotating
y = (x³ - 2x² + x) cos x around the x axis for