College algebra CHAPTER 3
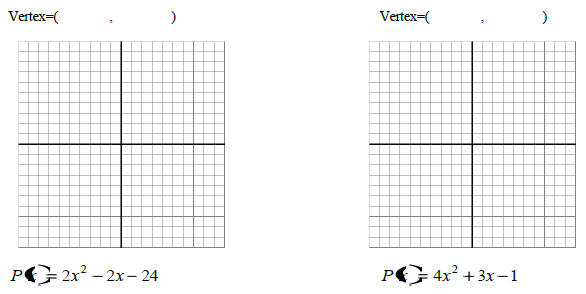
Find for each:
1. Horizontal moves (x)
2. Vertical moves(y)
3. Vertex
4. Up or down 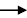 positive or negative positive or negative
5. write the probable equation
6. What is the maximum/minimum value of the function ?
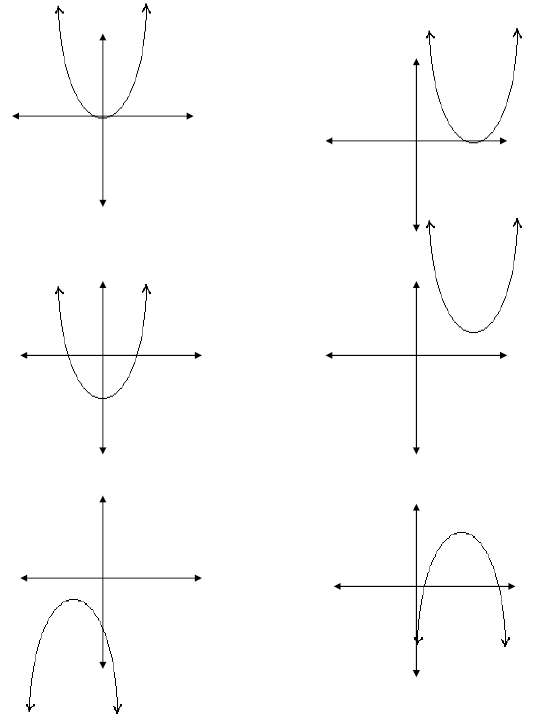
Completing the Square Warm Up:
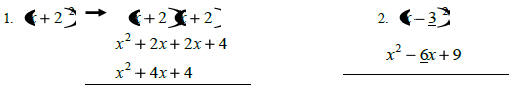

1. Look at the previous and fill in the blanks without
factoring:
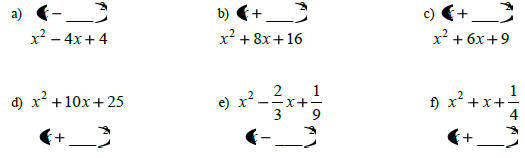
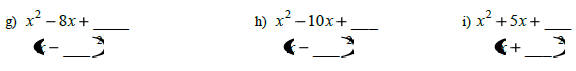
so,
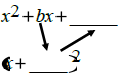
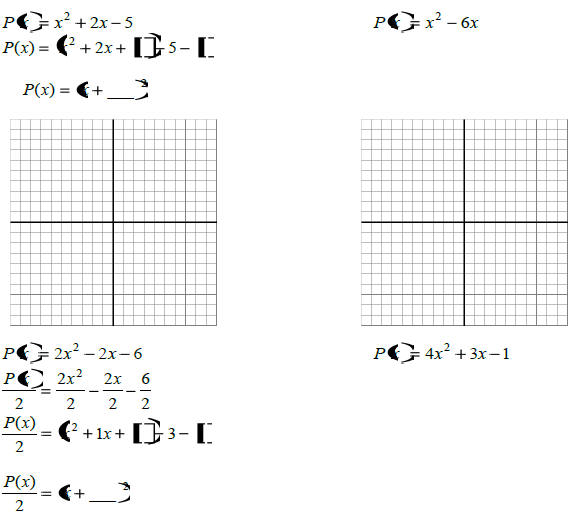
Vertex formula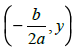

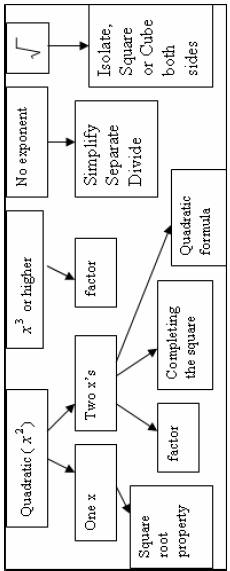
Zero factor property
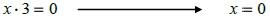 |
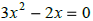 |
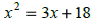 |
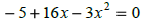 |
| Square root property (one x) |
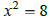 |
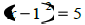 |
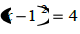 |
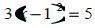 |
Quadratic formula ( two x ’s)
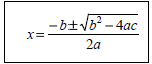 |
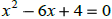 |
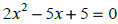 |
 |
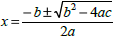
Discriminant --------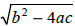 |
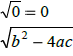
|
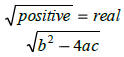
|
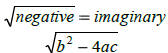 |
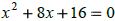 |
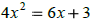 |
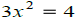 |
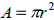 for r
for r |
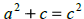 for c
for c |
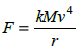 for v
for v |
 |
 |
 |
|
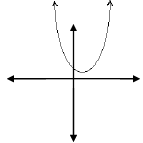
Solving quadratic inequalities
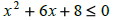
|
This is when infinitely many
solutions occur
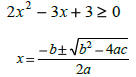
|
This is when a no solution occurs
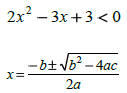
|
|
|
Check with x = 0 |
Check with x = 0 |
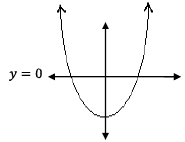
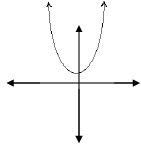
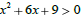 Let's look at this one graphically
Let's look at this one graphically
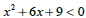 Let's look at this one graphically Let's look at this one graphically
 THE
SUM OF TWO POSITIVE NUMBERS
 |
So we basically have the following:
a) If one number is x , then the other number is __________________
b) The restriction on x is:
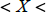
c) The function that represents the product of the two numbers is:
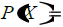
d) Find the maximum for the function and the
two numbers.
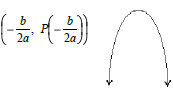
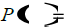
A farmer wishes to enclose a rectangular region
bordering a river with fencing, as shown in the diagram.
Suppose that x represents the length of each of the three parallel
pieces of fencing. She has 600 feet of
fencing available.
i) Finish the equation y + = 600
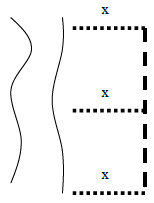
Solve for y =_________________
a) If the length of each of the three parallel pieces is x,
then the length of the remaining side in terms of x is:
b) The restriction on x is: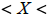
c) The function that represents the area of the
fenced region is: A= L times W = ______ times __________
d) Find the maximum area and the dimensions .
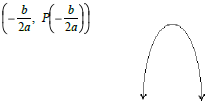
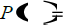
e) What would the dimensions be for an area of
22,500 square ft?
A piece of sheet metal is 2.5 times as long as it is wide. It is
to be made into a box with an open top by cutting 3-
inch squares from each corner and folding up the sides. Let x
represent the width of the original piece of sheet
metal.
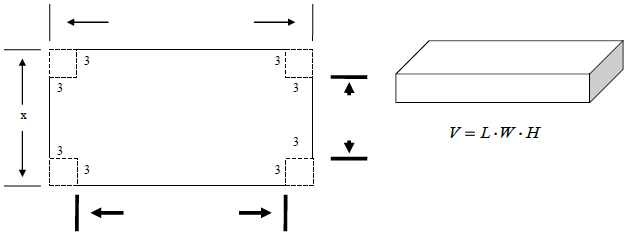
a) The restriction on x is x > 6 why?
b) Determine a function that represents the volume:
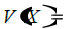
c) For what value of x will the volume of the box be 600?
e) For what value of x will the volume of the box be 800?
d) For what values of x will the volume of the box be between 600 and
800?
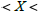
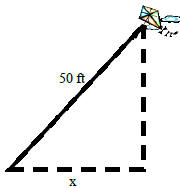
A kite is flying on 50 ft of string. How high
is it above the ground if its height is 10 feet more than the
horizontal distance from the person flying it? Assume the string is
being held at ground level.
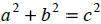
|
When Respect Brings Success charges
$600 for a seminar on management techniques, it attracts 1000
people.
For each decrease of $20 in the charge, an additional 100
people will attend the seminar. Let x represent the
number of $20 decreases in the charge.
a) Determine a revenue function R that will give revenue generated as a
function of x, the number of $20
decreases.
Revenue= Price X Number Sold
b) Find the value of x that maximizes the revenue.
What should the company charge to maximize the revenue?
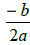
c) What is the maximum revenue the company can generate?
Graphing Polynomials
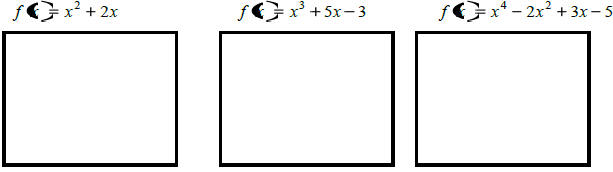
|
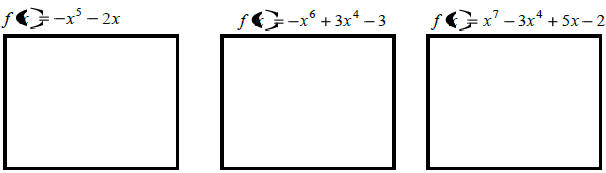
Draw the end behavior
| + leading coefficient , odd degree |
+leading coefficient, even degree |
| - leading coefficient, odd degree |
- leading coefficient, even degree |
EXTREMA
Local maxima--- the highest point at a peak.
Local Minima----the lowest point at a valley
Turning Point
Degree give the number of possible x-intercepts

Copy the graph from your calculator and locate and
label the local maxima and minima.

|
Absolute Maxima--- the highest
point at a peak is also the highest point on the graph.
Absolute Minima----the lowest point at a valley is also the lowest point
on the graph.
If there is an absolute maximum and/or minimum , then label them. |
| What are the x-intercepts?
Dividing by polynomials

Steps :
1)
2)
3)
4) |
| Synthetic division only when dividing
with the form of x – r.
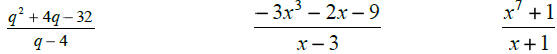 |
Find P(3) |
divide
 |
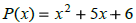
Find P(-2) |
divide
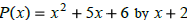 |
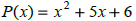
Find P(0.5) |
divide
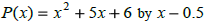 |
Remainder Theorem:
If a polynomial P (x) is divided by x-k, the remainder is equal to
P(k). |
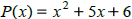
Find P(-2) |
divide
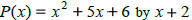 |
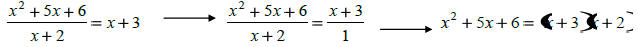
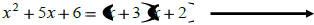
if x=-2 then 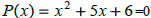
if x=-3 then 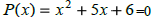
We call -2 and -3 Zeros of
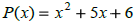 |
Determine if 3 is a zero of
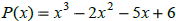 , use synthetic and the remainder
theorem , use synthetic and the remainder
theorem
This means that if 3 is a zero of 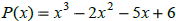
Then the factored form of 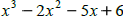 would
partially be would
partially be
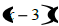
What would go into the parenthesis ?
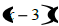
How would you find the remaining portion?
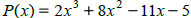 If one of the zeros is -5, then what
are the others? If one of the zeros is -5, then what
are the others?
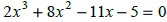
|
 |
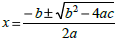 |
Intermediate Value Theorem
If one value of the polynomial is negative and one value is positive,
then there is zero
between those two values.
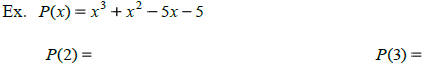
Review: 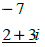 |
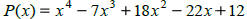 If
one of the zeros is 1-i, then what are the others? If
one of the zeros is 1-i, then what are the others?
The degree of the polynomial is __________. Which means there are
_________
possible distinct roots( they could repeat).
 |
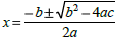
 |
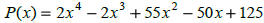 If
one of the zeros is-5i, then what are the If
one of the zeros is-5i, then what are the
others?
The degree of the polynomial is __________. Which means there are
_________
possible distinct roots( they could repeat).
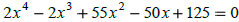 |
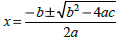 |
Find a polynomial of degree 3 that
has the following conditions:
(don't forget the constant) |
| 1) Zeros of -3, -1, and 4
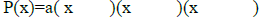 |
2) Zeros of -3, -1, and 4. P(2)=5 |
| 1) Zeros of 2 and 3i |
2) Zeros of 2 and 3i . P(0)= - 36 |
1) Zeros of
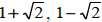 , and 3 , and 3
Finding Possible zeros.
Multiply 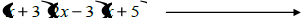
Zeros are |
 If one of the zeros is-5i, then what are the others?
If one of the zeros is-5i, then what are the others?
What are the possible Zeros?
Last number____. Factors of last number__________________________
First number____. Factors of first number__________________________
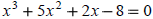
Factor
P(x) ______________________
|
|
| Graphing Polynomials By Hand |
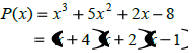
End behavior? ___________
Zeros?___________

|
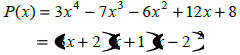
End behavior? ___________
Zeros?___________
|
| Solve. Find some of the zeros
graphically?
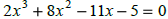
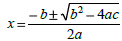
Solve. Find some of the zeros graphically?
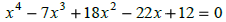
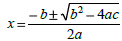
|
| Graphing Polynomials By Hand and
answer the questions |
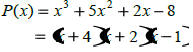
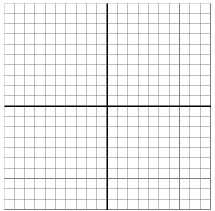
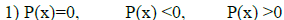
|
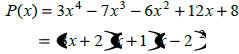
|
Start solving your Algebra Problems
in next 5 minutes!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
January 22nd
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
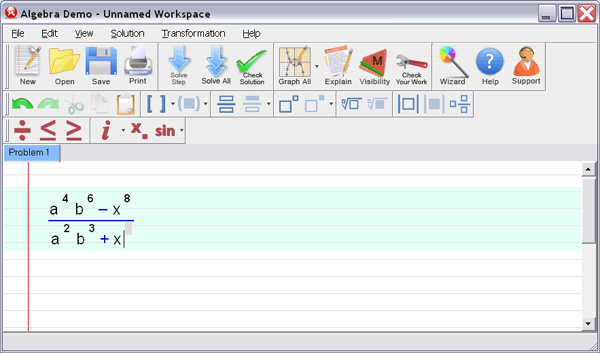
Step 2 :
Let Algebra Helper solve it:
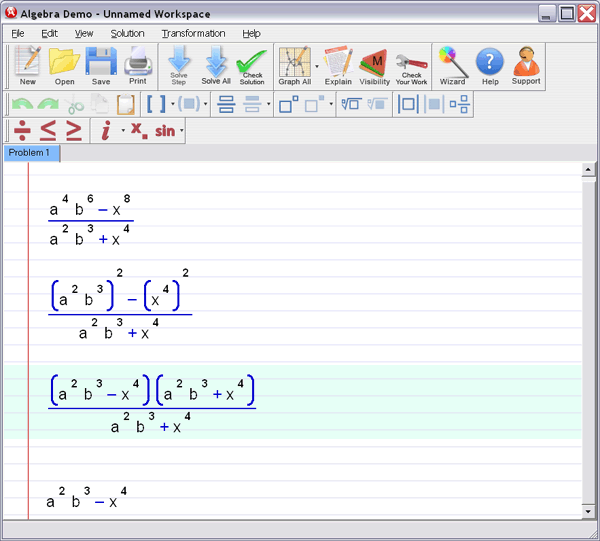
Step 3 : Ask for an explanation for the steps you don't understand:
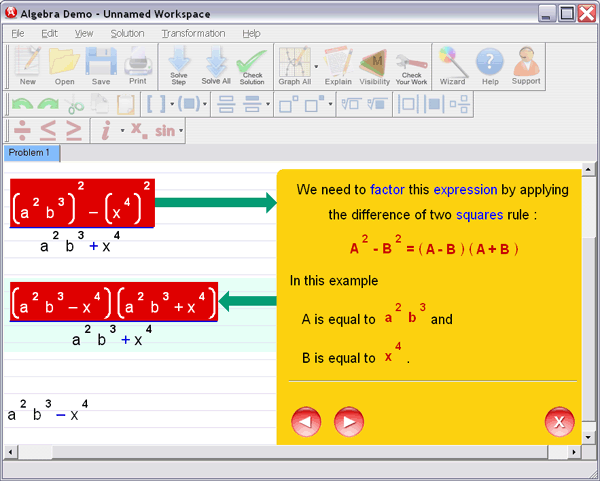
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |



