The purpose of the following 10 questions is to assess
some math skills that you will need in
Physics I. These questions will help you identify some math areas that you may
want to review
as you take Physics I. As always, select the best answer from the choices given.
1. Consider the following equation:
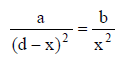
where a > 0, b > 0, and d > 0. We are looking for a
solution for x where 0 < x < d.
A. It is impossible to solve this equation except with
numerical techniques because it
involves the reciprocals of polynomials and there is no general formula for
that.
B. There is exactly one solution and it can be found using a linear equation.
C. There are exactly two solutions that are found using the quadratic formula.
D. It is possible to write an expression for the solution (s) using the quadratic
formula, but it
is impossible to know which one(s) (if any) satisfy the condition on x without
knowing
more about a, b, and/or d.
E. None of the above.
ANSWER
The correct answer is B. Most people taking this test realize that the equation
can be put into
the following form:
ax2 = b(d - x)2
There is a great temptation at this point to put this
equation into standard quadratic form and
use the quadratic formula. The problem can be solved this way, but it is easier
simply to take
the square root of both sides, which gives
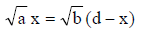
Since the conditions on the problem guarantee that both
sides of this equation are positive,
we don’t worry about the negative square roots . The solution is
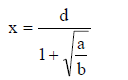
Could we solve this using the quadratic formula? Yes, but
neither C nor D is correct. After
some manipulation, the solutions using the quadratic formula are
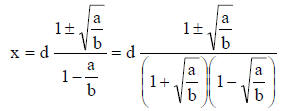
There are two solutions to this equation. One is the
correct solution given above. The other
is an incorrect solution:
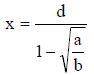
If a < b, then x > d. If a = b, then x is undefined. If a
> b, then x <0. In any case, this
solution does not satisfy the conditions on x. Therefore, there are not two
solutions (choice C
is incorrect) and it is possible to select the correct solution without knowing
more about a and
b (choice D is incorrect).
RELEVANCE TO PHYSICS 1
We will use this equation or similar equations to find
points in space where two gravitational
or electric forces cancel each other.
In questions 2-4, the function f(x) is continuous and
differentiable on the interval [a,b]. That
means that the graph of f(x) is a continuous curve with no breaks and the slope
of f(x) is well-defined.
When we speak of the slope of f (x), we mean the slope of the graph of f(x)
versus x.
2. If the slope of f(x) is negative in [a,b], then
A. f (x) ≤ 0 at all points in [a,b].
B. f (x) = 0 at some point in [a,b].
C. f (a) > f (b) .
D. All of the above.
E. None of the above.
ANSWER
C is the correct answer. If the slope of a function is negative throughout
an interval, it is
decreasing. A negative slope does not imply anything about whether the function
itself is
positive or negative .
RELEVANCE TO PHYSICS 1
We study graphs of displacement and velocity in Physics 1 and draw
conclusions from them.
3. If f(x) < 0 in [a,b], then the slope of f(x)
A. is always positive at all points in (a,b).
B. is always negative at all points in (a,b).
C. must be zero at some point in [a,b].
D. All of the above.
E. None of the above.
ANSWER
E is the correct answer. The fact that a function is negative does not imply
anything about its
slope.
RELEVANCE TO PHYSICS 1
We study graphs of displacement and velocity in Physics 1 and draw
conclusions from them.
4. In the interval [a,b], the slope of f(x) is constant.
The average value of f (x) in that interval is
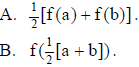
C. the area under the graph of f(x) between a and b, divided by (b–a).
D. All of the above.
E. None of the above.
ANSWER
D is the correct answer. C is the definition of the average of a function. A
and B are also
true for the special case of a function that has a constant slope, or in other
words the graph is
a straight line.
RELEVANCE TO PHYSICS 1
We can solve many kinematics problems if we plot velocity versus time and
take the area
under the curve as displacement. These math facts are particularly useful for
motion with
constant acceleration.
5. In the graph below (not necessarily to scale), f(x) is
defined in the interval [a,b] by the
straight line segments connecting the points as shown.
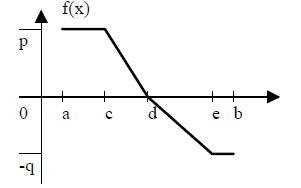
The area under the graph
A. is always positive or zero.
B. is zero if p = q.
C. can be calculated using area formulas for triangles and rectangles.
D. All of the above.
E. None of the above.
ANSWER
C is the correct answer. A is not true because the area under the curve of a
negative function
is negative. B is not true because we don’t have enough information about the
locations of
the points along the horizontal axis to draw that conclusion . While in general
we need
calculus to compute the area under a curve, in the special case of curves that
can be broken
into line segments we can use simple geometric area formulas instead.
RELEVANCE TO PHYSICS 1
We use the concept of area under a curve in Physics 1 to solve problems
involving
displacement, energy, and impulse.
6. The vector 
shown
below has length c. Its angle measured counter-clockwise from
horizontal axis is θ and its angle measured clockwise from the vertical axis is
.
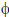The vertical component of
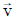is given by
A. c sin(θ).
B. c cos(90°–θ).
C. c cos().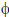
D. All of the above.
E. None of the above.
ANSWER
D is the correct answer. The equivalence of A, B, and C is a basic fact of
trigonometry.
RELEVANCE TO PHYSICS 1
All Physics 1 students should be comfortable with basic trigonometry for finding
components
of vectors.
