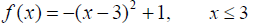Composite Functions; One-to-one Functions;
Inverse Functions
L13 Composite Functions; One-to-one Functions;
Inverse Functions
A composite function
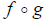(read as “f composed
with g”) is defined by
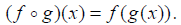
The domain of
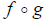is the set of all real x in the
domain of g for which g(x) is in the domain of f .
Example: Show a diagram for the composite function
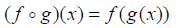
Similarly we define:
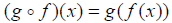
Example: Let
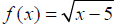and
g(x) = x^2 − 2. Find:
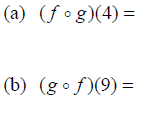
(c) Find the composite functions and their domains
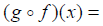
Domain:
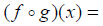
Domain:
Example: Using the tables, find
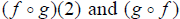(1).
What is the value of
?
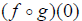Example: Find functions f and g such that
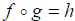if
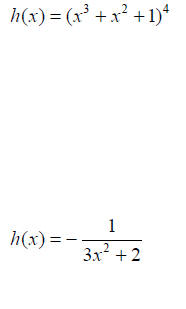
Example: An oil spill in the ocean assumes a circular
shape with an expanding radius r given by
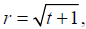
where t is the number of minutes after the measurements
are started and r is measured in meters.
(a) Find a formula that gives the area A of the circular
region as a function of time t.
(b) What is the area at the beginning? (t = )
(c) What is the area 3 minutes later? (t = )
Inverse Relations and Inverse Functions
Recall that a relation is a set of all ordered pairs (x, y),
where x is an element from the domain of the relation and
y is the corresponding element from the range.
Thus, the inverse relation we defined as the set of all
ordered pairs ( y, x).
Example: Find the inverse of the following relations.
Which of the relations are functions? Determine whether
the inverse relations are functions.
{(−2,2),(−1,1),(0,0),(1,1),(2,2)}
{(−2,8),(−1,1),(0,0),(1,−1),(2,−8)}
Note: Not for every function the inverse relation is a
function.
The inverse of a function is a function itself if and only if
for each y in the range there is only one x in the domain.
In other words, no two ordered pairs have the same
second coordinates , that is, no horizontal line intersects
the graph at more than one point.
The functions for which the inverses are also functions
are called one-to-one.
Horizontal Line Test
If each horizontal line intersects the graph of a
function f in at most one point, then f is one-to-one.
Example: Use the Horizontal Line Test to determine
whether the function is one-to-one.
Note: A function which is increasing/decreasing on an
interval I is one-to-one on I.
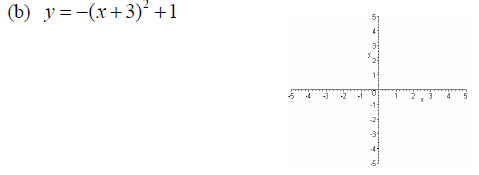
Note: A quadratic function y = a(x − h)^2 + k (a ≠ 0)
is not one-to-one, but, when considered on the restricted
domain, for example, on interval [h,+∞), it is one-to-one.
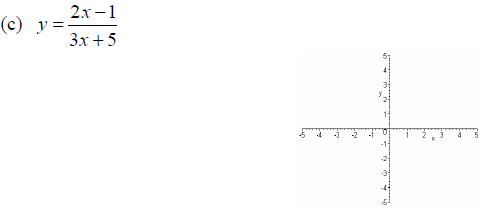
Inverse Functions
Remember, that the inverse of a function f is also a
function if and only if f is one-to-one.
Let f be a one-to-one function. Then g is the
inverse function of f if
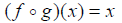for all x in the domain of g;
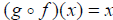for all x in the domain of f.
If g is the inverse function of f, then we write g as
f-1(x) and read: “f-inverse”.
Example: Determine whether the following functions are
inverses of each other:
Cancellation Rules for Inverses
The inverse functions undo each other with respect to
their compositions:
f-1( f (x)) = x for all x in the domain of f
f(f-1( y)) = y for all y in the domain of f-1
Equivalent Form of the Cancellation Rules:
| f (x) = y |
<-> |
f-1(y) = x |
| (x in domain of f) |
|
(y in the domain of f-1) |
Note on the Domains and Ranges of the Inverses:
Domain of f-1 = Range of f
Range of f-1 = Domain of f
Graphing Inverses :
If the graph of f is the set of points (x, y), then the
graph
of f-1 is the set of points ( y, x).
Since, points (x, y) and ( y, x) are symmetric with
respect to the line y = x
then
the graphs of f and f-1 are symmetric with
respect to
the line y = x.
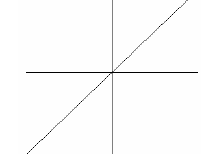
Example: Given the graph of
y = f (x). Draw the graph of
its inverse.
Finding the Inverse of a One-to-one Function f:
1. Write y = f (x).
2. Solve the equation for x : x = f-1( y)
3. Interchange x and y.
4. Give your answer in the form: y = f-1(x).
Note: Consider all restrictions on the variables .
Example: Find f-1(x) if it exists.
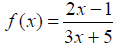
Finding the Inverse of a Domain-restricted Function:
Find the inverse of
