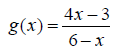One-to-One Functions and Their Inverses

Let f be a function with domain A. f is said to be one-to- one if no two
elements in A have the same image.
Example 1: Determine if the following function is one-to-one.
•A one-to-one function has an inverse function.
•The inverse function reverses whatever the first function did.
Example: The formula
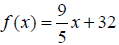
is used to convert from x degrees Celsius to y degrees Fahrenheit. The formula
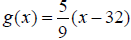
is used to convert from x degrees Fahrenheit to y degrees Celsius
•The inverse of a function f is denoted by f-1 , read “f-inverse”.
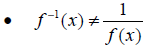
Example 2: Assume that the domain of f is all real
numbers and that f is one-to-one. If
f(7) = 9 and f(9) = -12, then what is
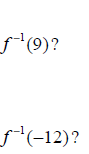
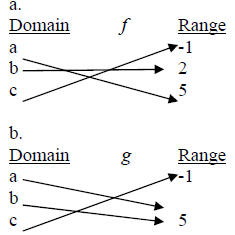
Example 3:
If f and g are inverse functions, f (-2) = 3 and f (3) = -2 . Find g(-2) .
Domain and Range:
The domain of f is the range of f-1 and the
range of f is the domain of f-1 .
These two statements mean exactly the same thing:
1. f is one-to-one (1-1)
2. f has an inverse function
Property of Inverse Functions
Let f and g be two functions such that ( f o g)(x) = x for
every x in the domain of
g and (g o f )(x) = x for every x in the domain of f then f and g are
inverses of
each other.
Example 4:
Show that the following functions are inverses of each other
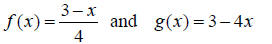
How to find the inverse of a function: (if it exists!)
1. Replace “ f (x) ” by “y”.
2. Exchange x and y.
3. Solve for y .
4. Replace “y” by “ f-1(x) ”.
5. Verify!
Example 5:
Find the inverse function of f (x) = 2x - 7 .
Example 6:
Assume f (x) is a one-to-one function. Find the inverse function f-1(x)
given that
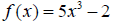
Example 7:
Find the inverse function f-1(x) given that
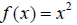
Example 8:
Assume g(x) is a one-to-one function. Find the inverse function g-1(x)
given that
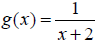
Example 9: Assume g(x) is a one-to-one function.
Find the inverse function g-1(x) given that