Increasing, Decreasing, and Constant Functions
Example 1: Determine the intervals on which the function in the figure at
the right is (a) increasing, (b)
decreasing, and (c) constant.
a) increasing on the interval ___________
b) decreasing on the interval ___________
c) constant on the interval ___________
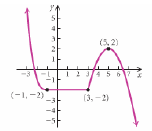
Notice that the intervals are written using only ______ (x or y)- values .
Relative Maximum and Minimum Values
To identify relative max and min values with your calculator:
1. Type the function into Y=.
2. Experiment with window settings as needed.
3. Go to the CALC menu by typing 2nd TRACE.
4. Choose either 3:minimum or 4:maximum.
5. Notice the question at the bottom left corner of your screen, “Left Bound?”.
Use your arrow
keys to move just to the left of the desired point. Type Enter.
6. You should now see “Right Bound?” at the bottom left corner of your screen.
Use your
arrow keys to move just to the right of the desired point. Type Enter.
7. You should now see “Guess?” at the bottom left corner of your screen. Type
Enter. (You
can move your cursor close to the relevant point first, but your calculator will
find the
maximum/minimum regardless.)
Functions Defined Piecewise
Do Example 5:
:
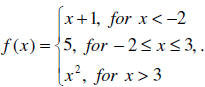
To find f (−5) , find which part of the function applies. Since − 5 < _____ , we
use the formula
f (x) = ____________ . Therefore, f (−5) = _______________ .
To find f (−3) , we use the formula f (x) = ____________ . Therefore, f (−3) =
_______________ .
To find f (0) , we use the formula f (x) = ____________ . Therefore, f (0) =
_______________ .
To find f (3) , we use the formula f (x) = ____________ . Therefore, f (3) =
_______________ .
To find f (4) , we use the formula f (x) = ____________ . Therefore, f (4) =
_______________ .
To find f (10) , we use the formula f (x) = ____________ . Therefore, f (10) =
_______________ .
Section 2.2 The Algebra of Functions , pp. 181-187,
Brief Summary
Sums , Differences, Products , and Quotients of Functions
If f and g are functions and x is in the domain of each function, then
Example 1a: Given that f (x) = x +1 and
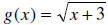, find ( f + g)(x).
( f + g)(x) =
Read p. 183, and find the domain of ( f + g)(x) .
Domain of f : __________ Shade in domain of f :
Domain of g : __________ Shade in domain of g :
Domain of f + g : __________ Shade in domain of f + g :
Notice that the domain of f + g is the set of numbers that are in both the
domain of f and the
domain of g.
Example 2a: Given that
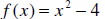and
g(x) = x + 2 , find the domain of f + g and f / g .
The domain of f is _____________________. The domain of g is
_______________________.
The domain of f + g is
_________________________________________________________.
For the domain of f / g we must exclude ______, since ______=______. Thus the
domain of
f / g is _______________________________________.
Difference Quotients
The difference quotient, or average rate of change, is the ratio
Example 3: For f (x) = 2x − 3, find and simplify the
difference quotient.
Section 2.3 The Composition of Functions, pp. 189-196,
Brief Summary
The Composition of Functions
The composite function f o g is defined as ( f o g)(x) =
____________________ where x is in the
domain of g and g(x) is in the domain of f.
Example 1a: Given that f (x) = 2x − 5 and
,
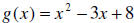find each of the following.
( f o g)(x)
(g o f )(x)
Decomposing a Function as a Composition
Example 4: If h(x) = (2x − 3)5 , find two functions f (x) and g(x)
such that h(x) = ( f o g)(x) . In other
words, if h(x) were the answer to a composition problem, what might the question
have been?
f (x) =
g(x) =
Check: ( f o g)(x) =
