Altitudes in a triangle: The altitudes of a triangle are
the Cevians that are perpendicular
to the sides. The three altitudes of an acute triangle are concurrent
at a point denoted by H and called orthocenter. If a triangle is obtuse, then
the
altitudes determine lines that are concurrent at a point also called orthocenter
which is not in the interior of the triangle.
Angle bisector: A ray, say OC, that is in the interior of
an angle, say ∠AOB,
which divides the angle in two equal parts (∠AOC = ∠COB) is called the angle
bisector of that angle.
Angle Bisectors of a triangle: The angle bisectors of a
triangle are the Cevians
determined by the angle bisectors of the three angles of the triangle. These
Cevians intersect at a point denoted by I and called incenter. This point is the
center of the circle inscribed in the triangle.
Perpendicular bisectors in a triangle: The perpendicular
bisectors in a triangle
are the lines perpendicular on the sides at their midpoint. These lines
intersect
at a point denoted by O and called circumcenter. This point is the center of
the circle circumscribed to the triangle.
Quadrilateral: A quadrilateral is a polygon with four
vertices (or four sides).
Trapezoid: A trapezoid is a quadrilateral in which two of
its sides are parallel.
Square: A square is a regular polygon with four sides.
Rectangle: A rectangle is a quadrilateral with all angles
having the same measurement.
Parallelogram: A parallelogram is a quadrilateral with two
pairs of parallel sides.
Kite: A kite is a quadrilateral in which the four sides
can be divided into pairs
of adjacent congruent sides.
Rhombus: A rhombus is a quadrilateral in which all the
sides are congruent.
Vertex Angle of a regular polygon: The vertex angle of a
regular polygon is the
angle formed by two consecutive sides. Given a regular polygon then its vertex
angles measures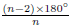 
where n is the number of
sides .
The central angle of a regular polygon: A central angle of
a regular polygon is
and angle whose vertex is the center of the polygon two rays corresponding to
two consecutive vertices of the polygon.
Collinearity test: Given points P, Q and R in the plane or
space then they are
collinear, with Q between P and R, if and only if PR = PQ + QR.
Slope of the line determined by two points: Given two
points P(x1, y1) and
Q(x2, y2) in the plane with an orthogonal system of coordinates, the slope of
the line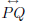 
is given by
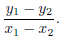
Slope and collinearity: Given three distinct points P, Q
and R in a plane, then
they are collinear if and only if the slopes of
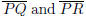are equal or undefined.
Midpoint formula: Given two points P(x1, y1) and Q(x2, y2) in the plane with
an orthogonal system of coordinates , then the midpoint of the segment
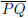is
the point of coordinates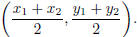 
Midquad Theorem: Given an arbitrary quadrilateral then the
midpoints of its
sides form a parallelogram.
Perimeter: The perimeter of a polygon is the sum of the
lengths of its sides.
Circumference: The “perimeter” (length of the curved line )
of a circle is called
circumference. Its formula is given by C = 2πR where R is the radius of the
circle.
Theorem about parallel and perpendicular lines: Two lines
are parallel (perpendicular)
if and only if their slopes are the same or undefined (the product of
their slopes is -1 or one line is vertical and the other line is horizontal).
Slope intercept equation of a line: The equation of a line
passing through the
point on the y-axis (0, b) and having slope m is y = mx + b.
Point-slope equation of a line : The equation of a line
passing through the point
P(x1, y1) and having slope m is y - y1 = m(x - x1).
Equation of a circle: The equation of a circle centered at
(a, b) and radius r has
the formula (x - a)2 + (y - b)2 = r2.
Area of a rectangle: The area A of a rectangle with
perpendicular sides of lengths
a and b is A = ab.
Area of a parallelogram: The area A of a parallelogram is
equal to the product
of one of sides (base) and the height corresponding to it: A = bh.
Area of a square: The area A of a square whose sides have
length s is A = s2.
Area of a triangle: The area A of a triangle with base of length b and
corresponding
height h is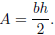 
Heron’s formula: The area of a triangle whose side lengths
are a, b, c is A =
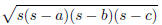where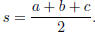 
Area of a trapezoid: The area A of trapezoid with parallel
sides of lengths a and
b and height h is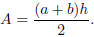 
Area of a disc: The are A of a disk of radius R is A = πR2.
Pythagorean Theorem: In a right triangle, if the legs have
lengths a and b and
the hypotenuse has length c, then a2 + b2 = c2.
Converse of the Pythagorean Theorem: If in a triangle ABC
with side lengths
a, b, c such that a ≤ b ≤ c we have
(1) a2 + b2 = c2 then the triangle is a right triangle
in C (∠C = 90°),or,
(2) a2 + b2 > c2 then ∠C < 90° and so the triangle is
an acute triangle, or
(3) a2 + b2 < c2 then ∠C > 90° and so the triangle is
an obtuse triangle.
Triangle inequality : If P, Q, R are points in a plane then
PQ + QR ≥ PR.
Pick’s Theorem: The area of a polygon whose vertices are
on a square lattice is
given by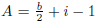 
where b is the number of lattice
points on the sides of
the polygon and i is the number of latices points inside the polygon.
A polygonal region is a polygon together with its
interior. The polygonal region
is called regular if the polygon at its boundary is a regular polygon.
By a region we understand a set of points in the plane.
The notion of interior
of a region is not defined in this course but it is a well defined concept in
the
branch of mathematics called Topology.
Covering of the plane: A covering of the plane is a
collection of regions with
the property that every two regions have no interior points in common and every
point in the plane belongs to at least one of these regions.
A tessellation is a covering of the plane with copies of
one or more but finitely
many regions. Every individual copy of those regions entering in a tessellation
is called a tile.
A regular tessellation is a tessellation with copies of
only one regular polygonal
region and every two tiles have no intersection or they may intersect along an
edge or at a vertex.
A semi - regular tessellation is a tessellation with
copies of at least two regular
polygonal regions, every two tiles have no intersection or they intersect along
an edge or at a vertex and at each vertex there is the same vertex arrangement.
Theorem about regular tessellations: There are only three
types of regular
tessellations: with regular 3-gons, regular 4-gons or regular 6-gons.
Congruent triangles: We say that two triangles are
congruent if there is a correspondence
between their vertices, say, 
such that all the corresponding six elements in the two triangles are congruent:
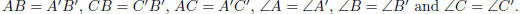
Cases of congruousness : (SSS), (ASA), (SAS) as in the
book and (SSA).
The SSA property: If two sides of an acute (respectively obtuse) triangle and
an angle which is not included are congruent, respectively, to two sides and the
corresponding angle of another acute (respectively obtuse) triangle, then the
two triangles are congruent.
Similarity of triangles and cases ofsimilarity : Two
triangles are similar if
their sides are proportional and their corresponding angles are congruent.
Theorem (AA) If two triangles have two pairs of congruent
corresponding
angles then these triangles are similar.
Theorem (SAS): if two triangles have two pairs of sides
proportional and the
angles in between are congruent then these triangles are similar
Square lattice: A square lattice is a set of points in a
plane which becomes
identical to the set of points of integer coordinates after a translation ,
rotation
or/and dilation.
Platonic Solids: Given a regular polyhedra then it can be
only of five types: a
cube , a tetrahedron, an octahedron, an icosahedron, or a dodecahedron.
Volume of a Parallelepiped The volume of a parallelepiped
is equal to the product
of the area of the base and the corresponding height:
V = (BASE AREA)(Height):
Volume of a pyramid: The volume of a pyramid is equal to
one third the product
of the area of the base and the corresponding height:
V = 1/3 (BASE AREA)(Height):
