In the automotive industry in this country, the fractions
you are most likely to see are known as proper
fractions. Proper fractions have the numerator (the top number) smaller than the
denominator (the bottom
number). Examples of proper fractions are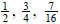 
Improper fractions are fractions in which the
numerator (the top number) is bigger than the denominator (the bottom number).
Examples of improper
fractions are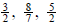 
Most people don't use improper
fractions. Instead, they use what's known as a
mixed number. Examples of mixed numbers are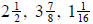 
There are three skills you need before you can work with
fractions.
The first is learning to reduce a fraction . Unless told
otherwise, fractions should always be reduced to the
lowest terms . This means divide the numerator and the denominator by a number
that is common to both.
This process is repeated until the fraction can't be reduced any further. For
example, consider the fraction
9/12. To reduce it, find a number that is common to both ; that is, a number that
can go into 9 and 12
evenly. For this example, that number is 3. (9 is 3x3x3 and 12 is 3x3x3x3
right?)
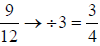
To reduce12/24 find a single number that goes evenly into
both the numerator and the denominator. There
are a few numbers that will work: 2, 3, 4, 6, and 12. Say you choose 3 as the
common factor. Then,
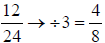
But notice that 4/8 can be reduced as well:
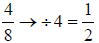
If you picked the greatest common factor, 12, instead of
3, you could have arrived at the fully reduced
fraction in one step . So divide top and bottom by 12:
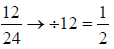
The next skill you need to learn is how to change an
improper fraction into a mixed number. To do this
divide the bottom number into the top number. Then write the remainder as a
fraction over the original
denominator. Then reduce the fraction if needed. For example to change 4/5 into
a mixed number, you
need to divide 4 into 5 and write the remainder (1 in this example) as the
numerator and the original
denominator (4 in this case) as the new denominator:
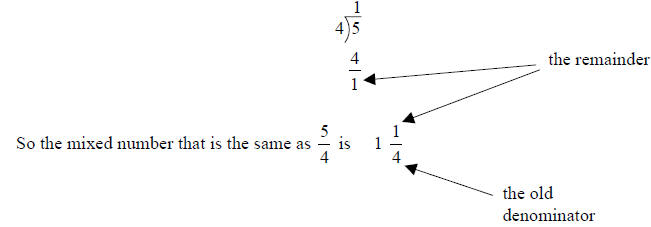
The third skill is learning how to change from a mixed
number to an improper fraction. This will be
necessary when multiplying or dividing fractions as we will see later in this
document. To do this first
multiply the denominator of the proper fraction by the whole number. Then add
the result to the
numerator. Then place the number you get over the original denominator. For
example, to change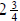 
into
an improper fraction, multiply the denominator (the 4) by the whole number (the
2) then add the result to
the numerator (the 3), and put the answer over the original denominator (4).
Multiply these two numbers together: 2 x 4 = 8.
Add that to the numerator; 8 + 3 = 11. Then place that number over
the original denominator to get the final answer:11/4
To multiply fractions simply multiple the numerators
together, multiple the denominators together, then
write the product of the numerators over the product of the denominators. Then
reduce the fraction to the
lowest terms . You can save a little time if you reduce the fractions you were
given before you multiply
them as well. You can also divide out a common factor from the numerator of one
fraction and the
denominator of the other. This will result in an answer that is already reduced
by that factor.
Example: Multiply 
Example: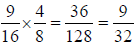
. You could
also have noticed that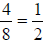 
. Then
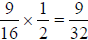. You could
have also chosen to divide out a 4 out of the 16 and the 4 in the original
fractions. That would leave you
with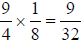 
. Which method you use is up to you.
When you want to multiply a fraction by a whole or mixed
number, do the following: First change all the
mixed numbers into improper fractions using the method described earlier.
Convert a whole number into a
fraction by putting the number over 1. Then multiply the fractions together as
before and reduce your
answer. For example:
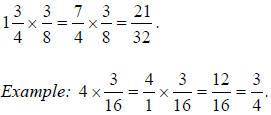
Homework Problems
In the following problems you will use what you’ve learned
about multiplying fractions. Be sure to
express your answers as reduced fractions or mixed numbers unless instructed
otherwise.
1. If you ask your co-worker to hand you the
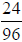inch wrench, which wrench should he bring
you?
2. If one piston from an engine weighs
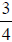pound, what do 8 pistons weigh? Write your
answer as a
mixed number with the fraction reduced to lowest terms.
3. A certain car requires
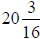inches of air conditioning hose. How many
inches of hose are needed
for 5 cars of the same type?
4. The cooling system of a Chevy 6 cylinder 250 cubic inch
displacement engine has a capacity of
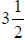gallons. If a solution of
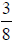ethylene glycol (the rest is water) is used
to protect the engine
against freezing temperatures, how many quarts of ethylene glycol are used?
Remember that there
are 4 quarts in 1 gallon.
5. A car has an average speed of
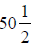miles per hour on a trip that lasts
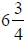hours. How far does the
car travel in this time? Hint: speed x time = distance traveled.
6. A car averages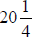 
miles per gallon of gas. How far can the car travel on
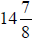gallons of gas?
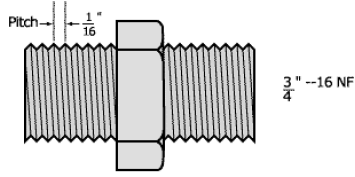
7. How far will the nut advance when it is turned 12 times
on 
inch--16 NF (National Fine
Thread) bolt? The nut advances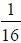 
" per
revolution on a 16 NF. The pitch refers to the distance
traveled by the nut in one turn (again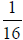 
" in
this exercise). On a 28 NF it would advance 
"
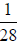per
revolution of the nut. See the figure. Note that the
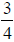” refers to the width of the bolt.
8. How far would a nut advance with 15 turns of a
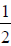inch--12 NC (National Coarse Thread) bolt?
9. A mechanic cuts 13 pieces of vacuum tubing from a roll.
Each piece is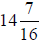 
inches long. What is
the total length used?
10. A autopainter works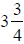 
hours re-painting your car and normally charges $35 per hour to work.
But because you are her friend, she only charges you
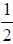her normal rate. How much do you owe
her?
