Derive for Windows, Version 4.10
Algebraic expressions in Derive 4 for Windows must be
“authored” before operators
can be applied to them. This is easy to do: simply click on Author
on the menu bar, then click on Expression and type in the desired expression.
Alternatively, you can use the icon on the toolbar corresponding to the Author,
Expression commands. In fact, the toolbar contains shortcuts for many of the
most frequently used commands.
Derive 4 for Windows numbers each line of input and output as it is created
on the screen. The first line is referred to as “#1,” the second as “#2,” and so
on. The line numbering system in Derive 4 for Windows makes it easy to refer
to any previously created expression, as you will observe in the accompanying
figures.
At any given time in Derive 4 for Windows, at least one line or part of a line
is highlighted. You can change the highlighted area by using the arrow keys to
scroll up or down. Some commands, such as Simplify, are designed to apply to
the currently highlighted expression. In Derive 4 for Windows the most recent
output line is highlighted by default, which makes it convenient to simplify the
most recently computed expression. For example, if line #6 contains a dot
product such as [2, −3, 4] · [−1, 0, −2], and if this dot product is highlighted
on
the screen, then clicking on Simplify and then on Basic produces a new line
(#7) containing the dot product −10.
Input of Vectors and Matrices; Fundamental Operations
To enter a vector or matrix, simply click on Author, and then on Vector or
Matrix. After indicating the dimension(s) of the vector or matrix, a template
of the correct size will form, which you fill in with the desired vector or
matrix
entries. Use the Tab key to move from entry to entry.
Use the “+” and “−” keys between vectors or matrices for addition and
subtraction , respectively. Place a scalar before a vector or matrix to perform
scalar multiplication . Use a “.” (period) between vectors to perform dot
product,
and between matrices to perform matrix multiplication. Use the “ ‘ ” (left
apostrophe) symbol after a matrix to calculate its transpose. The “^” symbol
is used to find powers of a ( square ) matrix. In particular, use “^(−1)” to
find the inverse of a (square) matrix. To convert fractions to decimals, use
the Approximate command, and specify the desired number of significant digits
displayed. These operations are illustrated in Figures D.7 and D.8.
| Input |
Output |
| Author,Vector,3,OK,5,Tab,7,Tab,-4,O |
#1: [5, 7, −4] |
| Author,Vector,3,OK,x,Tab,y,Tab,z,OK |
#2: [x, y, z] |
| Author,Expression,2#1+3#2,Simplify |
#3: [3x +10, 3y +14, 3z − 8] |
| Author, Expression,#1.#2,Simplify |
#4: 5x +7y − 4z |
Figure D.7: Derive 4 for Windows session: vectors;
fundamental vector operations
| Input |
Output |
Author, Matrix,3,4, OK,
4,Tab,-1,Tab,6,Tab,-2,Tab,
-3,Tab,2,Tab,-3,Tab,2,Tab,
-6,Tab,8,Tab,1,Tab,3,OK |
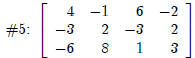 |
| Author,Matrix,4,3,OK,2,Tab,-3,(etc.) |
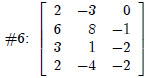 |
| Author, Expression,#5-2(#6‘),Simplify |
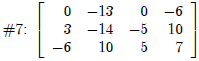 |
| Author, Expression,#5.#6,Simplify |
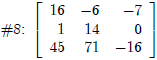 |
| Author, Expression,#8^(-1),Simplify |
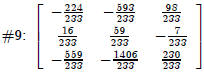 |
| Simplify,Approximate,4,Approximate |
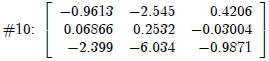 |
Figure D.8: Derive 4 for Windows session: matrices;
fundamental matrix operations
Solving a Linear System; Gauss-Jordan Row Reduction Method
You can solve a linear system directly using the Solve command. Click on
Solve and then System, and then indicate the number of equations to be solved .
A template will appear, into which you type each equation
in turn. Under the
template, indicate the variables to be solved for. If the system has no
solution,
the result “[ ]” will appear. If the system has more than one solution, each
independent variable will be represented with a differently numbered “@” symbol,
and the dependent variables will be expressed in terms of the independent
ones.
You can also solve a system using the row_reduce function. This function
computes the reduced row echelon form of a (possibly augmented) matrix. The
matrix on output line #12 below is the augmented matrix for a linear system
with an infinite solution set.
In Figure D.9, the same linear system is solved using both Solve and
row_reduce. You should verify that the general solution set obtained from
either method is equivalent to {(−3c+4, 2c +5, c, −2)}.
| Input |
Output |
Solve,System,4,OK,3x+y+7z+2w
=13,Tab,2x-4y+14z-w=-10,
Tab,5x+11y-7z+8w=59,Tab,
2x+5y-4z-3w=39,Tab
(x, y, z, w are highlighted), Simplify |
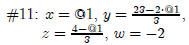 |
| Author,Matrix,4,5,OK,3,Tab,(etc.) |
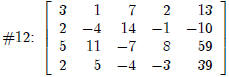 |
Author, Expression,
row_reduce(#12), Simplify |
 |
Figure D.9: Derive 4 for Windows session: solution of a
linear system; row reduction
Start solving your Algebra Problems
in next 5 minutes!
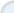 |
 |
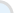 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
January 22nd
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
Step 2 :
Let Algebra Helper solve it:
Step 3 : Ask for an explanation for the steps you don't understand:
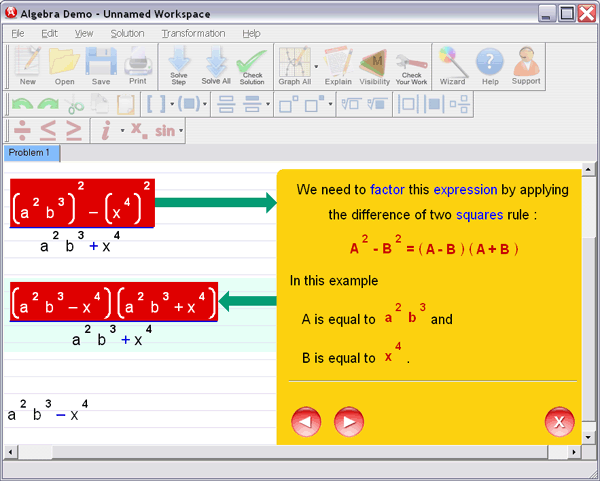
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |



