1 Floating-point numbers
In a digital computer, the set of real numbers R is approximated by a set of
floating-point numbers.
Representing a quantity as a floating-point number is very similar to
representing it using scientific
notation. In scientific notation, a number that has very large or very small
magnitude is represented
as a number of moderate magnitude multiplied by some power of ten. For example,
0.000008119
can be expressed as 8.119 ×10-6. The decimal point moves, or floats, as the
power of 10 changes.
A set of floating-point numbers F is defined by four integers.
β
the base
p the precision
[L ,U] the exponent range
A floating point number x ∈F is written as follows.
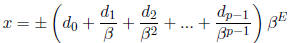
where E is an integer such that L≤ E ≤U
The string of base-β digits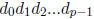 
is called the fraction. Notice that
the value of the precision
p determines how many digits there are in the floating-point number. The number
E is
called the exponent. A set of floating-point numbers is said to be normalized if
the lead digit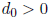 
unless the number represented is zero . In other words, in a normalized set of
floating point numbers,
a number has a lead digit of 0 if and only if that number is 0. In virtually
every modern
computer, floating point numbers are normalized and use base 2 (i.e. β= 2).
Internally to the
computer, a floating point number is represented by three integers. the sign
(1-bit), the fraction,
and the exponent.
A real number y ∈ R is not always exactly representable in a floating-point
system F . In this
case, y is usually approximated by x ∈ F where x = fl(y) is the closest
floating-point number to
y. This function fl is called round to nearest. In the case where two floating
point numbers are the
same distance from x, the nearest floating-point number ending in an even digit
is chosen.
2 IEEE Standard 754
The two sets of floating point numbers most commonly supported on modern
computer systems
are specified by IEEE Standard 754. They are.
IEEE single-precision. a base-2 (i.e. β= 2) system with 1 sign-bit, 8-bit
exponents, 23-bit fractions
and a bias of 127
IEEE double-precision. a base-2 (i.e. β= 2) system with 1 sign-bit, 11-bit
exponents, 52-bit
fractions and a bias of 1023
We denote the exponent as E, the sign-bit as S, the fraction as F and the bias
as b. The bias allows
the IEEE 754 standard to represent both positive and negative exponents . Assume
we have have a
bias of b where b is a positive integer. If the value of the exponent bits,
interpreted as an unsigned
integer, is E then the exponent of the floating-point number is E - b. The
fraction, F, can be
interpreted in two ways. When representing a normalized value, the fraction
represents the value
1.F where an implicit leading 1 is pre-pended followed by the radix point and
then the bits making
up F. When representing unnormalized values, the fraction is regarded as
representing 0.F . The
standard also includes special values used to represent
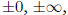and NaN which
stands for “Not a
Number”. We can summarize the rules for single precision IEEE 754 numbers as
follow.
1. If E = 0 and F = 0 then the value is 0 with S indicating positive or
negative.
2. If E = 255 and F ≠ 0, then the value is NaN.
3. If E = 255 and F = 0 then the value is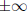 
with S indicating positive or
negative.
4. If 0 < E < 255 then the number represented is the normalized value
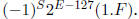
5. If E = 0 and F ≠ 0 then the number represented is the unnormalized
value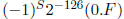 
Similar rules apply for double precision numbers, just replace E = 255 with E =
2047 and use
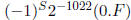for unnormalized values and
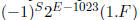for
normalized values.
3 Floating-Point Arithmetic
To add or subtract two floating-point numbers, the exponents must match before
the fractions can
be added or subtracted. If they do not match, the fraction of one must must be
shifted until the two
exponents match. As a result, the sum or difference of two floating point
numbers will not necessarily
be equal to the true sum of the two real numbers they represent. In other words,
since the
sum of two p-digit numbers can have more than p digits, the excess digits cannot
be represented by
a p-digit floating point number and will be lost. While multiplication and
division of floating -point
numbers does not require the exponents to match, these operations may also
produce answers different
from the corresponding operation on real numbers.
Since floating point operations only approximate
traditional arithmetic operations on real numbers,
they are often represented by different symbols :
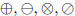, represent floating point addition,
subtraction, multiplication, and division respectively.
The associative law does not hold for floating-point numbers. The following laws
do.
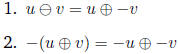
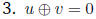if and only if v = -u
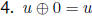
4 Problems
In answering the following questions, remember that in a binary number, binary
digits after the
“decimal point” are multiplied by successively smaller powers of 2, e.g.
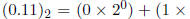
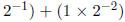. It may be useful to review section 3.6 of textbook which
discusses representing
integers in different bases.
1. Floating-Point Number Systems [10 points]
(a) A Small Set of Floating-Point Numbers
Suppose we create a simple normalized floating-point system F with
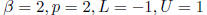
The smallest positive number we can represent in this system is
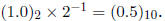
What is the largest positive number representable in the system?
How many numbers are in this system?
(b) Picturing Floating-Point Numbers
Using decimal notation, write out the entire set of numbers representable in the
floatingpoint
system described above (e.g. we have seen 0.5 is one of the numbers represented
in the system so it will be in the list you write out).
Now, draw a number line representing the real numbers in the interval [-3, 3]
and put
tick marks to show where the floating-point numbers in F fall on the line. Are
the
floating-point numbers uniformly distributed on the line ?
2. IEEE Standard Floating-Point Systems [15 points]
Answer the following questions for both single precision numbers and double
precision numbers.
(a) How many numbers are in the set?
(b) What is the smallest positive number that can be represented?
(c) What is the largest positive number that can be represented?
3. Round to Nearest [10 points]
Suppose we have a round to nearest function fl that maps real numbers to the
small floating
point system F described in Problem 1. Is this function one-to-one? Is it onto?
Justify your
answers. Hint. for one-to-one use a specific example, for onto you can write a
simple direct
proof showing that any x ∈ F has a real number that maps to it .
4. Arithmetic Operations [15 Points]
(a) We will prove floating-point addition is not associative. Suppose we have a
decimal (i.e.
β= 10) floating point number system with a precision of 8 digits that uses round
to
nearest. Under these conditions, we would have the following example.
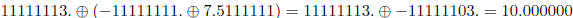
Show that a different answer is reached for
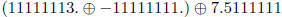
(b) Consider a 2-digit decimal number system in which uses round to nearest. In
this system,
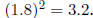Consider the algebraic identity
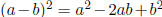. Is this
identity valid
in the number system we are using? To answer that question, try setting a = 1.8
and
b = 1.7 and calculate both the left hand side and the right-hand side of the
identity using
2-digit decimal arithmetic, rounding if necessary after each operation. What
answers do
you get?
(c) This problem involves fixed-point arithmetic but the lesson about the perils
of finite
precision are relevant for floating-point numbers as well. In 1982 the Vancouver
Stock
Exchange instituted a new index initialized to a decimal value of 1000.000. By
design,
indexed was fixed to always have three digits after the decimal point. After
each transaction,
a new index value was computed and truncated to three trailing decimal digits.
Twenty two months later, the value of the index should have been 1098.892.
Instead, the
calculated value was 524.881. In one or two sentences, explain what you think
caused
this inaccuracy.
