The ability to compute exactly or with high precision is one of the main
features of computer algebra .
The material in this lecture is based on [2, sections 2.3 and 2.4]. See also
[4]. For insight in multiprecision
arithmetic, we refer to [1, 3, 5].
3.1 Integers and Rational Numbers
Maple can handle very large integer numbers:
[> n1 := 3^(4^5),
Observe that the placing of the brackets matter:
[> n2 := (3^4)^5,
The largest integer number in MapleV had 219 -
9 digits. Since Maple 7, this limit was raised a bit:
[> md := kernelopts(maxdigits), # query a kernel variable
[> huge := 10^md: # may take time, depends on available memory
[> length(huge), # show number of digits
Note that we do not really wish to see this number,
therefore we close o with a colon, instead of a semicolon.
Let us try to push the limits:
[> huger := 10*huge:
Note that limitations of available memory may set the
limit on the largest number much lower than indicated
by the kernel variable maxdigits. Since Maple 9, the GNU Multiple Precision (GMP)
library is used for its
long integer arithmetic.
You may wonder what these huge numbers are good for. In
computational number theory, with the
applications in coding and cryptography, prime numbers play an important role.
For example the public key
RSA cryptosystem is based on the difficulty of factoring integer number into
primes.
Maple has fast algorithms to check whether a number is
prime or not:
[> n1 := 2^301-1, # a very large number
[> isprime(n1), # this is not a prime, but we
[> n2 := nextprime(n1), # can get the next prime number
[> ifactor(n2), # see if the number of prime
[> ifactor(n1), # this takes a long time...
While probabilistic algorithms exist to decide fast
whether a number is prime or not, to factor a number
in primes, one essentially has to try as many factors as the integer square root
of the number . In this case
the number of steps for this factorization is of the order of
[> isqrt(n1),
Notice the little `i' at the start of the commands ifactor
and isqrt to indicate that they operate on
integers and return integer results. Another important operation is the greatest
common divisor of two
integer numbers. In the assignments we will explore the capabilities of the
igcdex command, which solves
the extended gcd problem.
Maple automatically simplifies rational numbers so that
numerator and denominator are relatively prime
to each other:
[> a := 1234/4890, # numerator and denominator are even
[> gcd(numer(a), denom(a)), # shows simplification
3.2 Irrational and Floating-Point Numbers
Not all numbers have an exact representation. To get an
idea of the actual value of such numbers we
approximate using floating-point numbers.
By default, Maple shows 10 significant decimal places, as
the following experiment shows:
[> evalf(Pi),
[> evalf(Pi*1000),
[> evalf(Pi/1000),
So leading zeros are not counted as signi cant digits.
The number of digits determines the working precision of
the floating-point calculations in Maple , and in
particular the size of the roundo , for example:
[> r := evalf(5^(1/3)),
[> r^3,
As r is a floating-point approximation of the real cube
root of 5, we expected to see 5 as the result of the last
command, but the result was spoiled by roundo . To reduce the roundo we use more
decimal places. We
can do this in two ways: either adding the number of decimal places to the
argument of evalf, or assigning a
higher value to the variable Digits.
The floating-point arithmetic is in general software
driven, except in cases where Maple can deduce the
needed working precision for the value of Digits. Try this:
[> UseHardwareFloats,
Like Digits , UseHardwareFloats is another environment
variable which can be set by us to the values true,
false, or deduced. Concerning the last value, hardware floating-point arithmetic
can be performed when
Digits <= evalhf(Digits).
In applications where 14 or fewer decimal places suffice,
such as in plotting a function which is easy to
evaluate, hardware floating-point arithmetic is usually much faster. With evalhf,
we get access to the machine
arithmetic.
With the following experiment we illustrate the relevance
of using hardware oats. The piece of code
given below could be part of sampling the exponential function for plotting
purposes.
[> N := 10000: # number of samples
[> p := 20: # required precision
Depending on the actual speed of our machine, we can
increase the values for N and p to experience more
clearly the difference between software and hardware floating-point
calculations.
[> start_time := time(): # start recording CPU time
> for i from 1 to N do # loop from 1 to N
> a := evalf(exp(i),p): # take samples from the function exp
> end do: # terminate the loop
[> elapsed := time()-start_time, # display elapsed CPU time
Now we redo the calculation with hardware oats.
[> start_time := time():
> for i from 1 to N do
> a := evalhf(exp(i)):
> od:
[> elapsed := time()-start_time,
Observe the differences in elapsed times between the
software driven and hardware machine arithmetic.
3.3 Assignments
1. What happens when you type in 3^4^5, in a Maple
session? Why does Maple react in this way?
(Hint: consult ?operators[precedence].)
2. Write 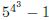 as a product
of primes .
as a product
of primes .
3. The greatest common divisor of two integer numbers a
and b can be written as a linear combination
(with integer coefficients k and l ) of a and b: gcd(a, b) = ka + lb.
In Maple this is achieved with the command igcdex. Look in
the help page of this command to compute
the coefficients of the linear combination of the greatest common divisor of
12214 and 2012. Give the
command you type in to find these coefficients and also give the command(s) to
verify the result.
4. In Maple, what is the difference between 1/3 + 1/3 +
1/3 and 1/3.0 + 1/3.0 + 1/3.0?
5. Consecutive rational approximations for
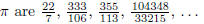
What is the next more accurate rational approximation for
π?
(Hint: search the Maple Help how to convert a oat to an
approximate rational number.)
6. Calculate 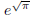 with 10,
20, and 30 decimal places accurately.
with 10,
20, and 30 decimal places accurately.
7. When calculating in high precision, we may want to
restrict the output. The number of displayed
decimal places is controlled by the interface variable displayprecision (consult
?displayprecision).
Set the display to four decimal places and execute sin(evalf(Pi)). Explain how
you can see from the
output of this command that the working precision is more than four decimal
places.
8. Explain the difference between 1.0+10^(-20) and
1+10^(-20) in Maple.
How can you make Maple return the same correct value of these two sums?
9. Set up an experiment to get an idea about the cost of
working with large number as the digits rise.
Consider the example of evaluating the exponential function N times at π for
increasing precision p.
Do the following calculations:
(a) Start with p = 10 and double the precision 7 times.
(b) Start with p = 20 and increase the precision 7 times with 20.
For both calculations, display the elapsed CPU time in a table.
10. By default, the working precision is 10 decimal
places. Find how to change this default globally,
without using the Digits command. (Hint: on Windows, look under Tools/Options,
on Unix, look
under File/Preferences, on Mac, look under Maple 12/Preferences.) Set it to the
more reasonable value
returned by evalhf(Digits).



