Reducing Rational Functions

Reducing Rational Expressions in x

Now that we’ve discussed some fundamental ideas and techniques, let’s apply what
we’ve learned to rational expressions that are functions of an independent variable
(usually x). Let’s start with a simple example.

Example 13. Reduce the rational expression

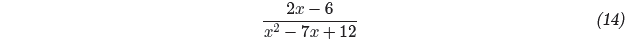
to lowest terms . For what values of x is your result valid?

In the numerator, factor out a 2, as in 2x − 6 = 2(x − 3).

The denominator is a quadratic trinomial with ac = (1)(12) = 12. The integer pair
−3 and −4 has product 12 and sum −7, so the denominator factors as shown.

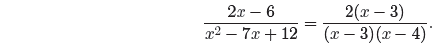
Now that both numerator and denominator are factored, we can cancel common factors.

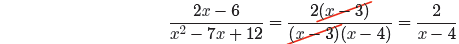
Thus, we have shown that

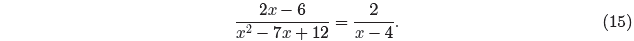
In equation (15), we are stating that the expression on the left (the original expression)
is identical to the expression on the right for all values of x.

Actually, there are two notable exceptions, the first of which is x = 3. If we
substitute x = 3 into the left-hand side of equation (15), we get

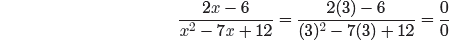
We cannot divide by zero , so the left-hand side of equation (15) is undefined if x = 3.
Therefore, the result in equation (15) is not valid if x = 3.

Similarly, if we insert x = 4 in the left-hand side of equation (15),

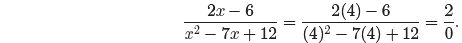
Again, division by zero is undefined . The left-hand side of equation (15) is undefined
if x = 4, so the result in equation (15) is not valid if x = 4. Note that the right-hand
side of equation (15) is also undefined at x = 4.

However, the algebraic work we did above guarantees that the left-hand side of
equation (15) will be identical to the right-hand side of equation (15) for all other
values of x. For example, if we substitute x = 5 into the left-hand side of equation (15),

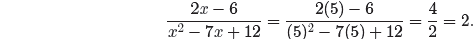
On the other hand, if we substitute x = 5 into the right-hand side of equation (15),

Hence, both sides of equation (15) are identical when x = 5. In a similar manner, we
could check the validity of the identity in equation (15) for all other values of x.

You can use the graphing calculator to verify the identity in equation (15). Load
the left- and right-hand sides of equation (15) in Y= menu, as shown in Figure 1(a).
Press 2nd TBLSET and adjust settings as shown in Figure 1(b). Be sure that you
highlight AUTO for both independent and dependent variables and press ENTER on each
to make the selection permanent. In Figure 1(b), note that we’ve set TblStart = 0
and ΔTbl = 1. Press 2nd TABLE to produce the tabular results shown in Figure 1(c).

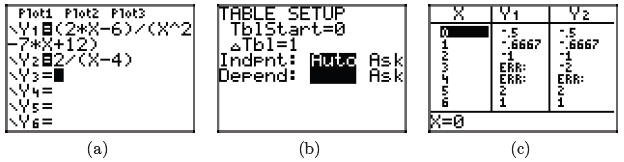
Figure 1. Using the graphing calculator to check that the left- and right-hand sides of
equation (15) are identical.

Remember that we placed the left- and right-hand sides of equation (15) in Y1 and
Y2, respectively.

• In the tabular results of Figure 1(c), note the ERR (error) message in Y1 when
x = 3 and x = 4. This agrees with our findings above, where the left-hand side of
equation (15) was undefined because of the presence of zero in the denominator
when x = 3 or x = 4.

• In the tabular results of Figure 1(c), note that the value of Y1 and Y2 agree for all
other values of x.

We are led to the following key result.

Let’s look at another example.

Example 16. Reduce the expression

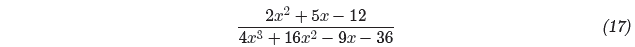
to lowest terms. State all restrictions.

The numerator is a quadratic trinomial with ac = (2)(−12) = −24. The integer
pair −3 and 8 have product −24 and sum 5. Break the middle term of the polynomial
in the numerator into a sum using this integer pair, then factor by grouping.

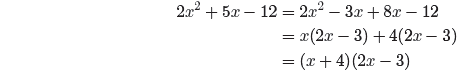
Factor the denominator by grouping .

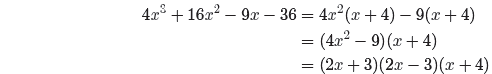
Note how the difference of two squares pattern was used to factor 4x² − 9 = (2x +
3)(2x − 3) in the last step .

Now that we’ve factored both numerator and denominator, we cancel common factors.

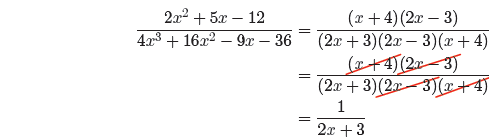
We must now determine the restrictions. This means that we must find those values
of x that make any denominator equal to zero.

• In the body of our work, we have the denominator (2x + 3)(2x − 3)(x + 4). If we
set this equal to zero, the zero product property implies that

2x + 3 = 0 or 2x − 3 = 0 or x + 4 = 0.

Each of these linear factors can be solved independently.

x = −3/2 or x = 3/2 or x = −4

Each of these x-values is a restriction.

• In the final rational expression, the denominator is 2x + 3. This expression equals
zero when x = −3/2 and provides no new restrictions.

• Because the denominator of the original expression, namely 4x³+16x²−9x−36, is
identical to its factored form in the body our work, this denominator will produce
no new restrictions.

Thus, for all values of x,

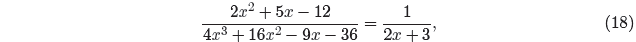
provided x ≠ −3/2, 3/2, or −4. These are the restrictions. The two expressions are
identical for all other values of x.

Finally, let’s check this result with our graphing calculator. Load each side of
equation (18) into the Y= menu, as shown in Figure 2(a). We know that we have
a restriction at x = −3/2, so let’s set TblStart = −2 and ΔTbl = 0.5, as shown
in Figure 2(b). Be sure that you have AUTO set for both independent and dependent
variables. Push the TABLE button to produce the tabular display shown in Figure 2(c).

Figure 2. Using the graphing calculator to check that the left- and right-hand sides of
equation (18) are identical.

Remember that we placed the left- and right-hand sides of equation (18) in Y1 and
Y2, respectively.

• In Figure 2(c), note that the expressions Y1 and Y2 agree at all values of x except
x = −1.5. This is the restriction −3/2 we found above.

• Use the down arrow key to scroll down in the table shown in Figure 2(c) to produce
the tabular view shown in Figure 2(d). Note that Y1 and Y2 agree for all values of
x except x = 1.5. This is the restriction 3/2 we found above.

• We leave it to our readers to uncover the restriction at x = −4 by using the up-arrow
to scroll up in the table until you reach an x-value of −4. You should uncover
another ERR (error) message at this x-value because it is a restriction. You get
the ERR message due to the fact that the denominator of the left-hand side of
equation (18) is zero at x = −4.