Properties for Exponents
If a is a real number , and r and s are integers, then
ar ×as = ar+s
Using Old Rules 22 × 23 = 4 ×8 = 32
Using New Rules 22 × 23 = 22+3 = 25 = 32
If a and b are two real numbers, and r is an integer, then
(a × b)r = ar × br
Using Old Rules (2 × 3)3 = (6)3 = 6
× 6 × 6 = 216
Using New Rules (2 × 3)3 = (2)3 × (3)3 = 8 ×27 = 216
If a and b are two real numbers with b ≠ 0, and r is an integer, then
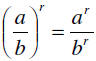
Using Old Rules
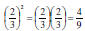
Using New Rules
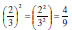
If a is any nonzero real number, and r is a positive
integer , then

Note: To remove the negative exponents that appear in a
problem, simply move then to
the opposite side of the division symbol .
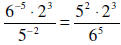
If a is any nonzero real number, and r and s are any two
integers, then
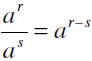
Using Old Rules
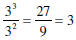
Using New Rules
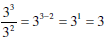
If a is any real number, then
a1= a
Note: Any base raised to the 1st power is
equal to the base.
Examples
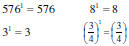
If a is any real number and a ≠ 0, then
a0 = 1
Note: Any base raised to the 0 power is
equal 1.
Examples
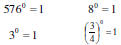
What is Scientific Notation?
▪ A way to write very, very large numbers
▪ A way to write very, very small numbers
Scientific Notation
A number is written in scientific notation
if it is written as the product of a number
between 1 and 10 and an integer power
of 10. A number written in scientific
notation has the form
n ×10r
where 1 ≤ n < 10 and r is an integer.
Writing in Scientific Notation
1) Move the decimal point to the right or left until you
have a
number that is greater than or equal to 1, but less than 10.
2) Count how many places you moved the decimal point . This
number will become the absolute value of the exponent .
3) If you moved the decimal point to the left, the exponent will
be positive.
4) If you moved the decimal point to the right, make the
exponent negative
Write the following number in decimal form.
5.75x10^4
This expression can be rewritten as 5.75x10x10x10x10
Furthermore

|
Write the following numbers
in scientific notation.
|
|
| a. 1043 |
a. 1.043x103 |
| b. 2.5 |
b. 2.5x100 |
| c. 0 000495 |
c. 4.95x10-4 |
a. The decimal is to the right of the 3. Move it left 3
places.
Solutions
b. This number is already greater than or equal to one and less
than 10. Therefore, the decimal doesn’t have to be moved
and the exponent will be 0
c. Move the decimal right 4 places.
1) Decide whether the number is in scientific notation. If not, tell
why the number is not in correct scientific notation
a. 0.54x103
b. 2.2x100.3
c. 8.0x105
A. This number is not written correctly in scientific
notation.
The value of c is supposed to be greater than or equal to 1and
less than 10. Here, the value of c is less than 1.
C. This number is correctly written using scientific
notation
2) Write the following numbers using scientific notation:
a. 7234
b. 0.085
c. 1.11
A. 7.234x103
B. 8.5x10-2
C. 1.11x100
3) Write the following numbers in decimal form:
a. 2.75x10-2
b. 8.375x106
A. 0.0275
The decimal point had to be moved two places to the left
because the power of ten was negative two.
B. 8375000
The decimal point had to be moved six places to the right
because the power of ten was positive six



