questions
First assignment: For next class, make a list of any questions you
have regarding the syllabus. If you have no questions, bring in a
sheet of paper that says "I understand and agree to the syllabus
for MTH 103.202," sign it , and date it. This is worth 5 points.
equations and expressions
Definition
An equation consists of two algebraic expressions joined by an
equal sign.
For example, in the equation
2 + 2 = 5
the left hand side is the expression 2 + 2 and the right hand side is
the expression 5. This particular equation is false, or inconsistent.
We're interested in a type of equation called linear equations .
linear equations
Definition
A linear equation in one variable, x is an equation of the form
ax + b = 0
where a and b are real numbers , and a is not 0.
For example,
4x + 12 = 0
is a linear equation in the variable x .
3t - 1 = 0
is a linear equation in the variable t.
linear equations - 2
Definition
To solve an equation means to tell every possible value of the
variable which makes the equation true. These values make up the
solution set for the equation.
For example, the linear equation
x = 0
is true exactly when we plug in 0 for the variable x. Any other
value of x makes the equation false.
We write that the solution set is {0}.
linear equations - 3
It's possible for more than one equation to have the same solution
set.
For example, consider the equation
3x = 0
It also has solution set {0}!
We say that the equations x = 0 and 3x = 0 are equivalent.
Definition
Two equations are equivalent if they have the same solution set.
linear equations - 4
In fact we're not just interested in equations which are of the form
ax + b = 0, but also equations which are equivalent to them .
For example, the equation
3x + 1 = 1
has solution set {0}, so it's equivalent to 3x = 0 and x = 0.
We'll call equations like 3x + 1 = 1 linear equations, too.
manipulating linear equations
Equations like x = 0 and t = 4 have obvious solutions ({0} and
f4g, respectively) so the strategy for solving a linear equation is
going to be to the equation into this form.
How do we do this?
The nice thing about the equals sign is that, as long as we do the
same thing to both sides, we won't change the truth of the
equality.
So, making sure to always do the same thing to both sides, we will
try to get our equation to look like t = 4.
manipulating linear equations - 2
What manipulations can we do to an equation? We can add or
subtract numbers:
3x + 1 - 1 =1 - 1
3x + 0 =0
3x =0
We can multiply or divide by numbers:
3x ÷ 3 =0 ÷ 3
x =0
We have just shown that the solution of 3x + 1 = 1 is {0}.
manipulating linear equations - 3
We might also have to add or subtract variable expressions , as in
2 - 4t + 4t =8 + 2t + 4t
2 + 0 - 8 =8 + 6t - 8
- 6 ÷ 6 =6t ÷ 6
- 1 =t
The solution is {-1}.
solving linear equations
There is a general strategy for solving linear equations. Consider
3(t - 2) = 6t + 7
1. We need to set up each side of the equation as a sum of terms :
3t - 6 = 6t + 7
2a. We collect all the variable terms on one side of the equation:
-6 = 6t + 7 - 3t
2b. We collect all the constant terms on the other side:
-6 - 7 = 6t - 3t
3. Simplify:
-13 = 3t
4. Divide to get
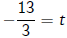
solving linear equations - 2
There is one last, and very important, step: checking the answer.
Our solution is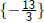 
, so we plug this in for t:
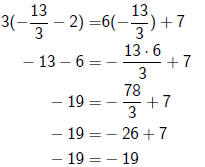
which it just so happens is a true statement. So our
solution is
correct.
solving linear equations - 3
To recap, solving a linear equation involves four steps:
1. Simplify to get a sum of terms on each side
2. Collect constants on one side and variables on the other
3. Combine each side's terms
4. Multiply or divide to get variable = constant
and the additional step of checking the answer.
In fact this same strategy can be used to solve equations which
aren't linear, but resemble linear equations.
solving equations with variable denominators
We want to solve equations like
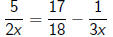
in which variables appear in the denominator.
We have to be careful, though. In this particular example, what
happens if we try the value x = 0?
We get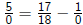
.
But division by zero is undefined, so this equation doesn't make
sense! ((We'll talk about why next class.))
So at the very beginning of the problem, we have to make sure we
aren't diving by zero. Here that means we can't let x = 0.
solving equations with variable denominators - 2
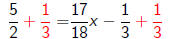This is a linear equation!
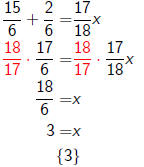
and we notice that our requirement x ≠ 0 is satisfied by
this
solution.
solving equations with variable denominators - 3
Let's try
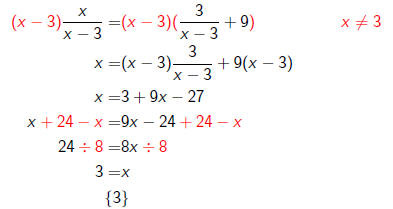
But our restriction is x ≠ 3, so this solution is invalid.
The
equation is inconsistent.
We write that the solution is Ø ?.
questions?
applications
What good is all of this? Well, it turns out plenty of things in life
can be modeled by linear equations.
A lot of them have to do with money.
applications - example
I'm going to pay you to do your homework. I'll pay 8
cents for each problem you get right, but you owe me 5
cents for each problem you get wrong. You do 26
problems, hand in your work, and I tell you we're even.
How many problems did you get right?
First pick something to be the variable. In this case, let's take c to
be the number of problems you got correct.
Then write the information given in terms of that variable.
The total number of answers is 26, so the number of incorrect
answers is 26 - c.
Now we can write down an equation.
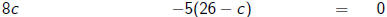
money from right ans. minus money from wrong ans. is zero
applications - example - 2
So we're left with the equation
8c - 5(26 - c) = 0
8c - 130 + 5c = 0
13c - 130 + 130 = 0 + 130
13c ÷13 = 130 ÷13
c = 10
Recall that c was the number of correct answers we gave. So our
answer is 10 correct answers.
Smell test: does our answer make sense in the original wording of
the problem?
Check the math:
8 · 10 - 5(26 - 10) = 0
80 - 130 + 50 = 0
-50 + 50 = 0
applications - interest
We'll come across the problem of interest in several guises.
Definition
The simple interest earned on an investment of P, at the annual
rate r , for t years, is I = Prt
You have $1000. You invest part of it at a simple interest
rate of 5%, the rest at a simple interest rate of 8%. At
the end of one year, you have earned $56 in interest.
How much did you invest in each account?
Pick a variable. x is the amount invested at 5%
Then 1000 - x is the amount invested at 8%
interest at 5% plus 
interest at 8%
is total
interest
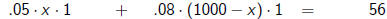
applications - interest - 2
So we need to solve
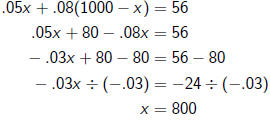
The question was "How much did you invest in each account?", so
we need to answer accordingly.
$800 was invested at 5%; $200 was invested at 8%.
Does the answer make sense in the context of the original
problem? Does the math check?
