Your Name:
Partner(s): 1.
2.
Over the next few days, factoring polynomials is our
focus . Unfortunately, no magic wand or
algorithm exists for factoring polynomials. However, one method that some
students find
particularly useful is the box method. Here’s how it works. Suppose we begin
with a quadratic
polynomial in factored form (x + 2)(x + 4). We can represent the product as the
area of a
rectangle of length x + 2 and width x + 4.
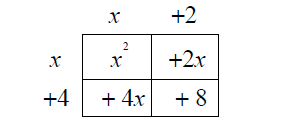
By combining the two linear terms on the diagonal, we get the product x2 + 6x
+ 8.
For factoring, we want to work backwards. We begin by placing the quadratic
term x 2 and the
constant term 8 in the upper left box and lower right box, respectively.
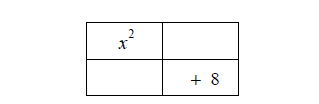
Next, we are trying to find the two terms that will go in the upper right and
lower left. To do
this we will use another schematic, the DIAMOND. In the top of the diamond we
place the
product of the first term and the last, (x2)(+8)= 8x2. In the bottom we place
the middle term,
6x.
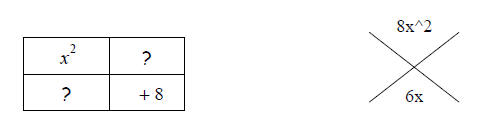
We are looking for the two terms whose product is 8x2 and whose sum is 6x.
You can start the
search by looking at possible factors of 8x2. These two terms are placed in the
sides of the
diamond and also give us the terms to fill in the box.
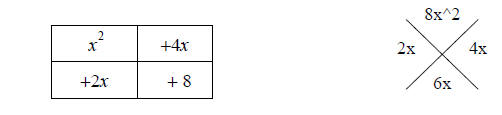
Now we continue by factoring out the greatest common factor (GCF) of the
terms in the first
row (or the first column):
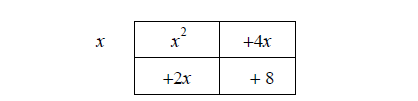
Then we ask what times x will be x2 which gives the term above the first
column, and what times
x will be 4x which gives the term above the second column.
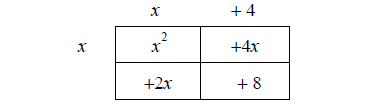
Then fill in the term left of the bottom row in a similar manner.
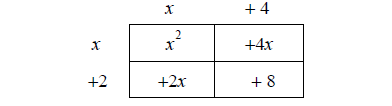
This will give the factored result.
x2 +6x + 8 = (x + 2)(x + 4)
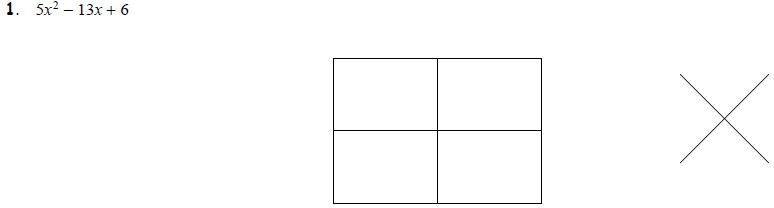
Task 1: Factoring Trinomials of the Form x2 + bx + c Factor the following
quadratic
trinomials using the box :






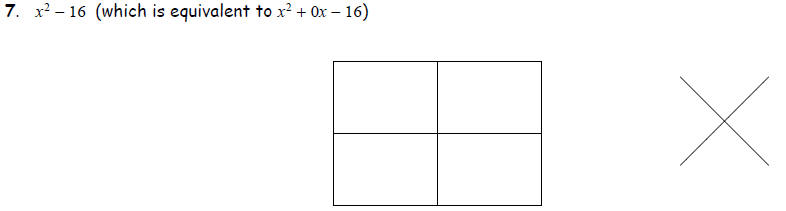
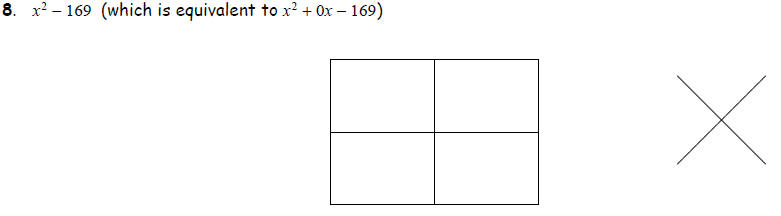
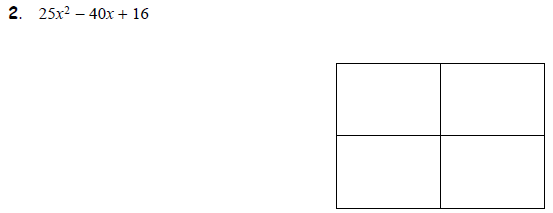
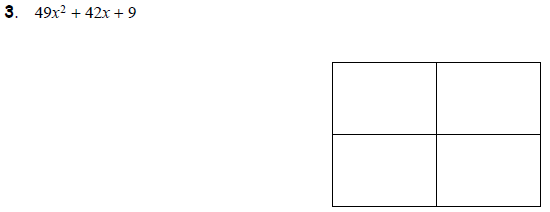
Task 2: Factoring the Difference of Squares and Perfect Squares The box can
be used
to factor differences of squares and perfect squares where the leading
coefficient is not 1.
Here, the diamond may not be very useful Instead, try to guess what term times
itself will give
the first term and what times itself (or its opposite) will give the last term.
Try these.
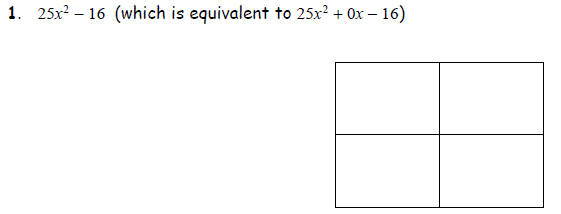
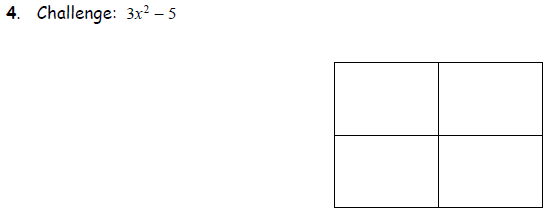
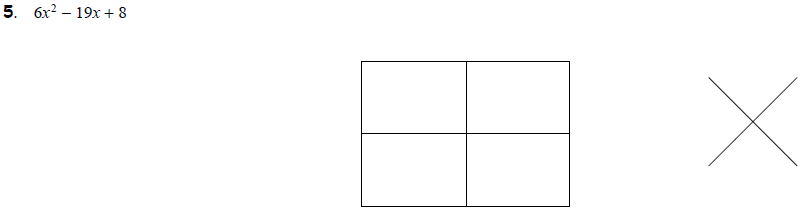
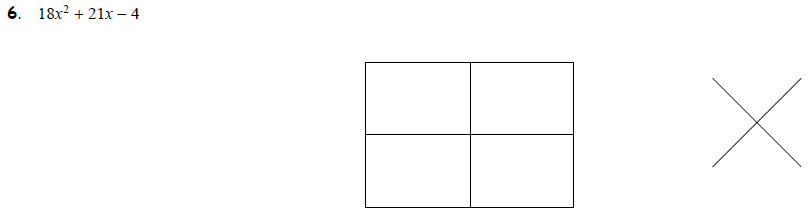
Task 3: Factoring Trinomials of the Form ax2 + bx + c These can be a little
more tricky to
do using the box, but the diamond can help. In fact, for these problems, using
the box serves
more as a way of organizing our work so that we avoid making errors. For
example, try the next
four examples:

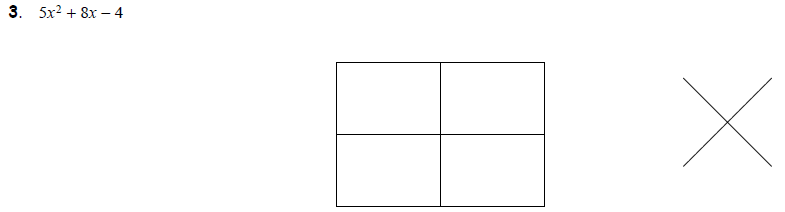
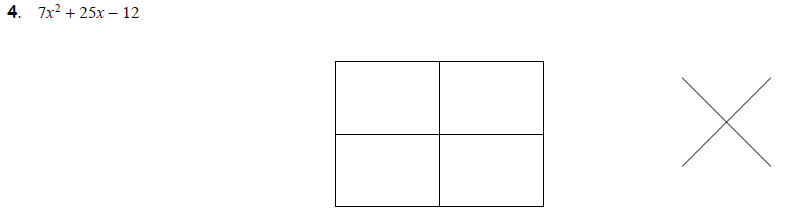
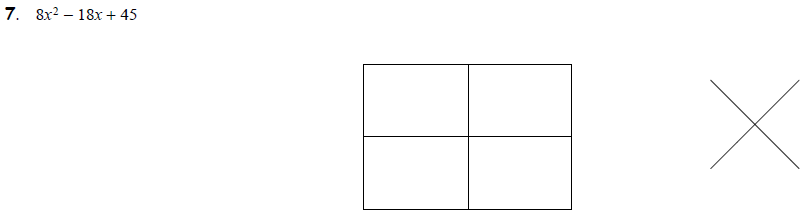
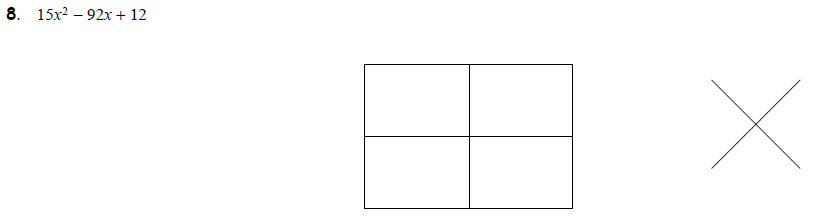
But sometimes, there are many choices. These examples
might take a few tries
before you get it right:
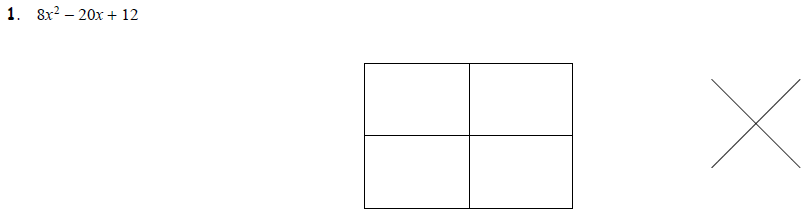
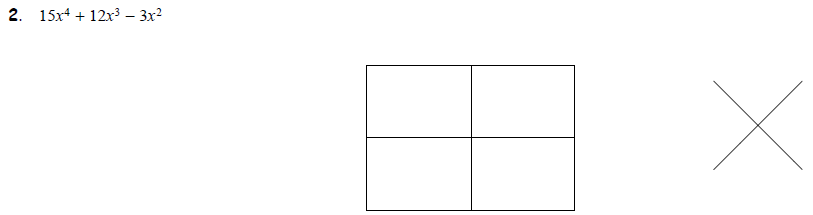
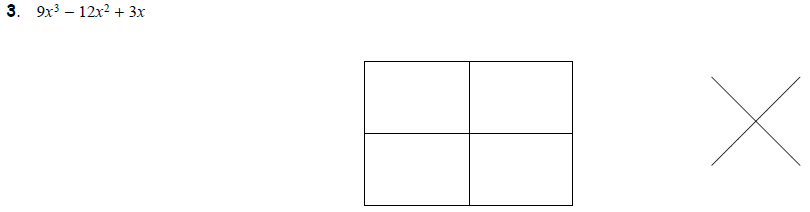
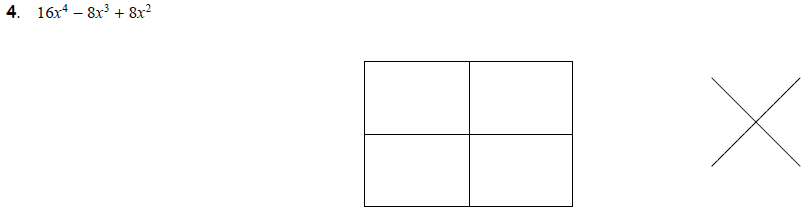
Task 4: Simple Factoring First, then the Box Finally,
the four examples below remind us
that factoring out a GCF first can make the factoring process much simpler.