Exercise 1 (20 points). Prove or disprove: For any three
sets A,B,C,
(a) C \ (A ∩ B) = (C \ A) ∩ (C \ B).
(b) C ∪ (A ∩ B) = (C ∪ A) ∩ (C ∪ B).
Solution
(a) The statement is false. A counterexample is: A = {1}, B = {2}, C = {1, 2}.
Then C\(A∩B) = {1, 2}
but (C \ A) ∩ (C \ B) = Ø;.
(b) The statement is true. We will first show that C ∪ (A ∩ B)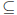 (C ∪ A) ∩ (C ∪
B). Consider any e
(C ∪ A) ∩ (C ∪
B). Consider any e
which is an element of the C \ (A ∩ B). Then e ∈ C or e ∈ A ∩ B. If e ∈ C, then
e ∈ C ∪ A and
e ∈ C ∪ B, so e is an element of the (C ∪ A) ∩ (C ∪ B). If e 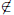 C, then e
must be in A ∩ B to still be
C, then e
must be in A ∩ B to still be
in the (C ∪ A) ∩ (C ∪ B). But then e ∈ A, which implies e ∈ C ∪ A, and similarly
e ∈ C ∪ B, so e is
still an element of the (C ∪ A) ∩ (C ∪ B). This proves C \ (A ∩ B)
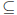 (C ∪ A) ∩ (C
∪ B).
(C ∪ A) ∩ (C
∪ B).
Now we show that C ∪(A∩B) 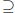 (C ∪A)∩(C ∪B). Consider any element e in the (C ∪A)∩(C
∪B).
(C ∪A)∩(C ∪B). Consider any element e in the (C ∪A)∩(C
∪B).
Since e must be an element of C ∪ A, it must be in C or in A. If e ∈ C, then e
must be in the
C \ (A ∩ B) too. If e 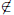 C, then we necessarily require e ∈ A for it to still be
in C ∪ A. Also, e must
C, then we necessarily require e ∈ A for it to still be
in C ∪ A. Also, e must
be in C ∩ B, so if e 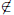 C then e must be in B.
So e ∈ A ∩ B, and hence e is in the C \ (A ∩ B). So
C then e must be in B.
So e ∈ A ∩ B, and hence e is in the C \ (A ∩ B). So
C \ (A ∩ B)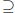 (C ∪ A) ∩ (C ∪ B).
(C ∪ A) ∩ (C ∪ B).
Putting the two results together, we have proved that C ∪ (A ∩ B) = (C ∪ A) ∩ (C
∪ B).
Exercise 2 (20 points). You have been appointed Postmaster General for a new
nation. Your job is to
determine what denominations to issue stamps in. Unfortunately, the government
wants to be able to
charge an amount for each letter or package that corresponds exactly to its
weight, so the postage fee could
be any integral number of cents . The government is also cheap and wants to
reduce costs by only printing
a minimal number of types of stamps, and stamps of value less than 5 cents will
not be allowed.
(a) What is the minimum number n of integer values
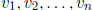 (where
(where 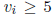 for all i) such that
for all i) such that
all positive integers can be expressed as linear combinations of them? What is
the precise condition
that such a minimal set 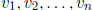 has to satisfy? Prove. Does your
answer apply to real life ?
has to satisfy? Prove. Does your
answer apply to real life ?
(b) Suppose the government caps the lowest possible package charge at c cents,
for some c > 50. In a
“real life” scenario, what is now the minimum number of stamp values
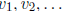 (where
(where 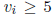 for
for
all i) that you can get away with so as to cover all package weights greater or
equal to c? Prove.
Solution
(a) The minimum number of values is n = 2. The precise condition is that
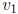 and
and
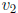 are coprime, namely
are coprime, namely
gcd(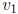 ,
, 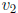 ) = 1. To prove, invoke Theorem 4.4.2, that an integer is a linear
combination of
) = 1. To prove, invoke Theorem 4.4.2, that an integer is a linear
combination of 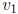 and
and
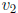 iff it is a multiple of gcd (
iff it is a multiple of gcd (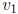 ,
, 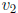 ). Thus if gcd(
). Thus if gcd(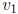 ,
, 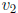 ) = 1, all positive
integers can be a linear
) = 1, all positive
integers can be a linear
combination of 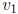 and
and 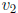 since all positive integers are a multiple of 1. And if
gcd(
since all positive integers are a multiple of 1. And if
gcd(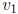 ,
, 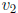 ) > 1, then 1
) > 1, then 1
is not a multiple of the GCD and cannot be represented.
(Note that almost everyone forgot to show
this: this is what the comments “prove other direction” or “prove necessity”
referred to.) Finally, it
won't work in “real life” because to represent values such as 1 requires
negative coefficients , and in
real life you can't to put negative amounts of stamps on letters.
(b) The minimum number is still 2. The simplest way is to use 5- and 6-cent
stamps. To prove that
this works, note that all integers c > 50 can be written as 5n + 1, 5n + 2, 5n +
3, 5n + 4, 5n + 5 for
some integer n ≥10. We can prove by induction on these five types that they can
all be a linear
combination of 5 and 6 with nonnegative coefficients. For base cases (n = 10):
51 = 9 × 5 + 1 × 6
52 = 8 × 5 + 2 × 6
53 = 7 × 5 + 3 × 6
54 = 6 × 5 + 4 × 6
55 = 5 × 5 + 5 × 6
Now assume that for n = k, that 5k+1 is a linear combination of 5 and 6 with
nonnegative coefficients,
so 5k + 1 = a × 5 + b × 6 with a, b ∈ N. If we consider n = k + 1, then 5(k + 1)
+ 1 = 5k + 6 can be
represented as (a+1)×5+b×6, so it is also a linear combination with nonnegative
coefficients. The
inductive step is exactly the same for the other four cases, so if 5k + 1, 5k +
2, 5k + 3, 5k + 4, 5k + 5
can be represented than so can 5(k +1)+1, 5(k +1)+2, 5(k +1)+3, 5(k +1)+4, 5(k
+1)+5. This
concludes the proof by induction.
Exercise 3 (20 points). Given a nonzero rational number r and two irrational
numbers a and b, prove or
disprove:
(a) ab is irrational.
(b) ar is irrational.
(c) ab is irrational.
Solution
(a) The statement is false. An immediate counterexample is
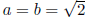 . We know
. We know 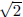 is irrational, but
is irrational, but
the product ab = 2 is rational.
(b) The statement is true. Proof by contradiction: Assume ar is a rational
number 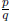 , where p, q ∈ Z, q ≠
, where p, q ∈ Z, q ≠
0. Since r is rational, it can be written as 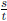 , s, t ∈ Z, t
≠ 0. Then
, s, t ∈ Z, t
≠ 0. Then 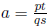 . Now r ≠ 0, so s ≠ 0, and
. Now r ≠ 0, so s ≠ 0, and
hence qs ≠ 0. pt and qs are both integers, and the latter is non- zero , so
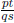 is rational. This implies
is rational. This implies
a is rational, which contradicts our assumption. Hence the product is always
irrational.
(c) The statement is false. Here are two ways to disprove it:
i. Consider 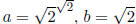 . Then ab = 2, which is rational. We know b to be irrational, but a's
. Then ab = 2, which is rational. We know b to be irrational, but a's
status is unclear. If a is irrational, then we have an immediate counterexample.
If a is rational,
then we have a counterexample cd, where c = d =
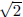 are irrational but the product (a) is
are irrational but the product (a) is
rational. Either way, we have shown that an irrational power of an irrational
may be rational.
ii. Consider a =
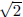 ,
,
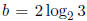 . Then ab = 3, which is rational. We know a is irrational, and
. Then ab = 3, which is rational. We know a is irrational, and
so is 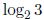 from Theorem 3.1.2 in the lecture notes. By part (b), b is
irrational and we have a
from Theorem 3.1.2 in the lecture notes. By part (b), b is
irrational and we have a
counterexample. (A very similar method can be used to show that
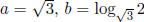 , which
, which
was one of the solutions you came up with during the midterm, works.)
Note: Euler's identity, 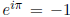 , is not a counterexample: irrational numbers are
a subset of the real
, is not a counterexample: irrational numbers are
a subset of the real
numbers, so an imaginary number like i does not count as irrational.
Exercise 4 (20 points). A perfect number is a natural number n ≥ 2 with the
property that the sum of
all of n's divisors (including 1, but not n itself) is n. 6 and 28 are the first
two examples. Prove that if
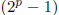 is prime, then
is prime, then
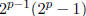 is a perfect number . Using this property,
find another perfect number
is a perfect number . Using this property,
find another perfect number
besides 6 and 28.
Solution The only prime factors are 2 and
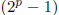 . The powers of 2 range from 0
to p - 1. Thus the
. The powers of 2 range from 0
to p - 1. Thus the
only factors are 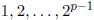 and
and
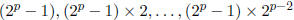 (The second sequence stops at
(The second sequence stops at
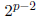 since we are omitting the number itself.) We can then write the sum of
factors as
since we are omitting the number itself.) We can then write the sum of
factors as
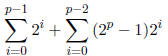
The right sum can be factored out giving
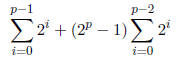
Now we can use a fact about sums of powers of 2 (this is a specific example of
the sum of a geometric
series):
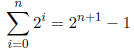
(In your solutions, you were not required to prove this. You can prove it fairly
simply by induction). If we
apply this identity twice, we have
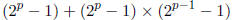
This simplifies to
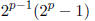
so the sum of the number's factors is the number itself and thus
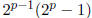 is
a perfect number.
is
a perfect number.
To find another perfect number, note that the next prime
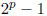 is 31 when p =
5. Plugging this into
is 31 when p =
5. Plugging this into
the formula gives 16 × 31 = 496.
Exercise 5 (20 points). Consider n planes in 3-dimensional space so that no two
are parallel, any three
have exactly one point in common, and no four have a common point . What is the
number of 3-dimensional
parts into which these planes partition the space? Prove. (You can use the
2-dimensional result without
proof.)
Solution The problem is solved much like the 2-dimensional
version. Consider adding the i-th plane (call
it plane P) and counting how many new regions it creates. Two nonparallel planes
intersect along a line,
so the other i-1 planes all produce intersection lines on P. The conditions that
no two planes are parallel,
any three have one point in common, and no four have a common point imply that
on P, no intersection
lines are parallel and no three lines have a common point. Thus we can apply the
two-dimensional result
and say that plane P is divided into 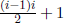 regions by the i-1 lines produced from the intersections of
regions by the i-1 lines produced from the intersections of
the other planes. Each region of P divides one of the existing regions of
3-space created by the first i - 1
planes in two, so adding the ith plane adds 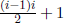 regions. Recalling that there is one region before any
regions. Recalling that there is one region before any
planes are added, we can then write the number of regions as
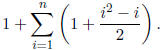
We can break up this sum into a sum over 1, i and i2. Obviously
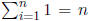 . We know from the
. We know from the
lecture notes that
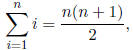
and from midterm practice that
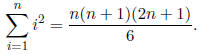
(As in problem 4, you were allowed to use these without proof.) Substituting
these in, the number of
regions for n planes is
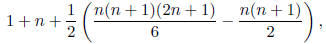
which simplifies to
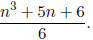
Much like the two-dimensional version, this can be formalized as a proof by
induction.



