Financial Mathematics Preparation Course Notes on
Calculus
1 The Real Numbers
The basis of calculus is the set of real numbers which we
shall denote by
the symbol R . Loosely speaking the real numbers is the set of all infinite
decimal expansions a0.a1a2a3a4 . . . where the ai’s are integers and ai
for
i ≥ 1 is between 0 and 9. Clearly all integers and all rational numbers
p/q where p and q are integers, q ≠ 0 are real numbers (for instance the
integer −124 can be written −124.000000 . . . ,1/3 = 0.33333333 . . . ). We
denote the set of integers . . . ,−3,−2,−1, 0, 1, 2, 3, 4, 5, . . . by the
symbol
Z and the set of all rational numbers by Q. The set of positive integers
1, 2, 3, 4, 5, . . . , n, . . . is called the set of natural numbers and is
denoted N.
We have N ⊂ Z ⊂ Q ⊂
R.
Both the natural numbers, the integers and rational
numbers have the
property of being countable i.e. we can write them all down in a sequence
z1, z2, z3, . . . , zn, . . . . For instance we can write down all the
integers in the
sequence 0, 1,−1, 2,−2, 3,−3, 4,−4, . . . . It is a little more tricky to see
that
the set of all rational numbers are countable but it can be done. The real
numbers, however are not countable. Here is the argument: assume that
R is countable and assume we have written down all the real numbers in a
sequence:
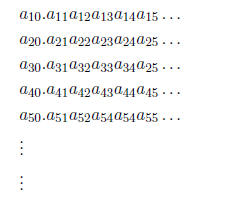
Thus the first index indicates the position in the sequence and the second
the position in the decimal expansion. We shall show that this is impossible
by constructing a real number which is not in this sequence. Choose b1 ≠
a11, b2 ≠ a22, b3 ≠ a33, b4 ≠ a44, b5 ≠ a, b6 ≠ a66, . . . . Now
form the
real number 0.b1b2b4b4b5b6b7b8 . . . . Assume this number is the n’th
term in
the sequence. Thus 0.b1b2b3b4 . . . bn · · · = an0.an1an2 . . . ann . .
. , but since
bn ≠ ann they are not equal and so we have a contradiction. Since the
rational numbers, Q, is countable this shows that there are strictly more
real numbers than rational numbers: Q ⊆ R. Here is
another argument,
which goes all the way back to the ancient greeks, that shows that there are
real numbers which are not rational: consider the real number
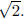 . If this is
. If this is
a rational number we can write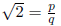 where we
assume that the fraction
where we
assume that the fraction
p/q is in lowest terms i .e. the integers p and q have no common factors. By
squaring both sides we get 2 = p2/q2 or by cross-multiplying 2q2 = p2. This
show that p2 is an even number, now if p itself was odd p would be of the
form 2r +1 for some integer r and so p2 = (2r +1)2 = 2r2 +1+4r which is
also odd. Hence in order for p 2 to be even p itself must be even so p = 2r.
But then p2 = 4r2 and we get 2q2 = 4r2. Dividing by 2 on both sides we
get q2 = 2r2 so q2 is even and hence also q must be even. This shows that
2 is a common factor in p and q in contradiction with the fact that p/q is in
lowest terms .
Real numbers can be added , multiplied and divided (if the
number we
divide by is ≠ 0) just as rational numbers can. What sets the real numbers
apart from the rational numbers, and which is the discovery that forms the
foundation of calculus is the concept of a limit. This notion took some 2000
years to discover. The ancient greek mathematicians studied geometry and
certainly discovered the number π as the ratio between the circumference
of a circle and its diameter. They were, however incapable of computing
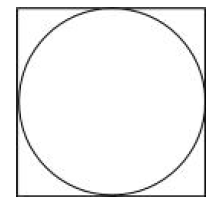
Figure 1:
π because as we now know π is not a rational number. The greeks were
certainly comfortable with some non-rational numbers as they freely operated
for instance with square roots but as we also know now π cannot be
expressed even using square roots (or any other kind of roots, third, fourth,
etc).
Example 1.1 We want to compute the area of the unit
disc i.e. the disc
with radius 1
Inscribing the disc in a square with sides = 2 we get that
the area
≤ 4 We divide the disc into 4 equal slices and divide the interval into
two halves . We inscribe the quarter circle in the union of two rectangles
as q shown in fig.2. The height of the smaller of the two rectangles is
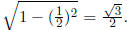 Thus the combined area of the two rectangles
is
Thus the combined area of the two rectangles
is 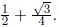
It follows that the area of the disc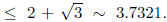 Next we
divide
Next we
divide
the interval into quarters and draw four rectangles: the height of the
rectangles are 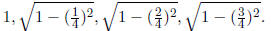 The combined area is
The combined area is
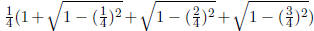 and so we get the estimate: area
and so we get the estimate: area
of the disc 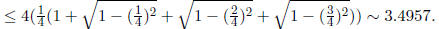
In the next step we divide the intervals into 1/8’ths and
we get the
combined area of the eight rectangles is 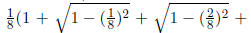
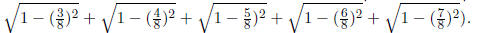 From this
From this
we get the estimate: area of disc ≤ 3.3398
We can continue this way, next we divide into 1/16’ths,
1/32’ths,. . . , 1/2n, . . . .
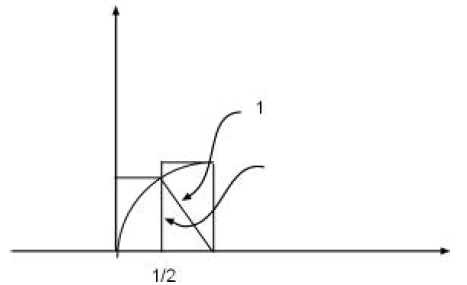
Figure 2:
In the n’th step the combined area of the 2n rectangles
is
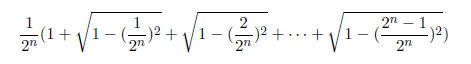
Thus we get the estimate: area of disc 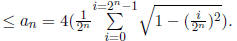 We
We
can see from the figures that the rectangles fit better and better around the
disc and so w can continue this process and approximate the area of the disc
as closely as we want. Using MATLAB we can easily compute the terms in
this sequence (at least as many as our computing power allows )
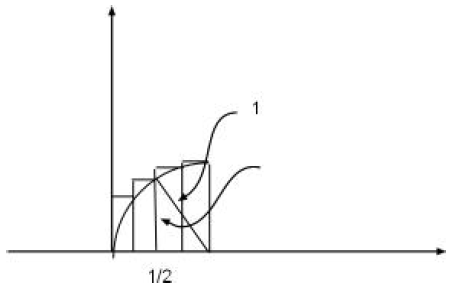
Figure 3:
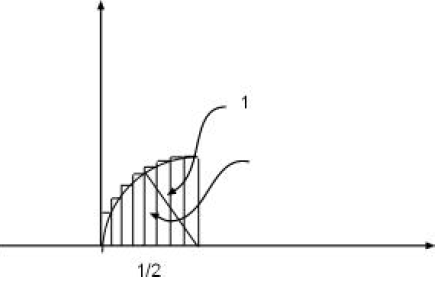
Figure 4:
Here are the 25 first terms

Type in the following code as an M-file in MATLAB and use
it to compute
some of the numbers in this sequence:
function y=A(n)
v=0:2^ n;
S=sqrt(1-((2^ n-v)/2^ n).^ 2);
y=4*(1/2^ n)*sum(S);
MATLAB gives the following value for π = 3.14159265358979
and as we
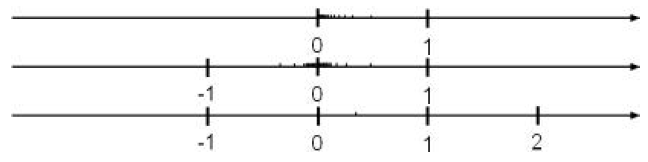
Figure 5:
know the area of the unit disc is π it certainly looks
likely that the terms in
this sequence approaches π as n becomes larger
The notion that a sequence of real numbers approach
another real number
is fundamental in calculus and we need a formal definition of what it means.
Before we give the formal definition let us consider a few more examples of
sequences.
Example 1.2 1. an = 1/n

Thus the sequence {an} is 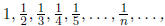 the sequence {bn}
is
the sequence {bn}
is
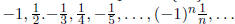 and {cn} is the sequence
and {cn} is the sequence
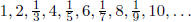
We see that the terms in both {an} and {bn} ”cluster”
around 0 but while
half of the terms of {cn} cluster around 0 the other half grows larger and
larger.
It is this clustering behavior we shall use to give a
strict mathematical
definition of what it means for a sequence of real numbers to ”approach” a
fixed real number a.
Definition 1.0.1 Let {an} be a sequence of real
numbers. We say that {an}
converges to a real number a (notation: an → a for n → ∞
or 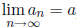
if no matter how close we are to a, all the numbers in the sequence except
for at most finitely many are even closer to a. This is the definition in
words. In mathematics we have to make precise the notion of being close.
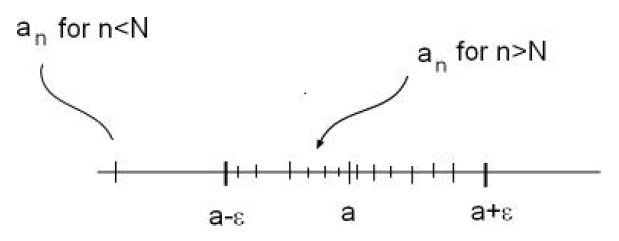
Figure 6:
Let ε be a positive real number (you should think of ε as
a very small positive
number). The numbers which are ε close to a consists of the real numbers x
such that the distance between x and a, |a − x| is smaller than ε. Thus the
real numbers ε close to a is the set {x|a − ε < x < a + ε} = (a − ε, a + ε).
The definition of convergence means that no matter how small an ε > 0
we take all but finitely many terms in the sequence are ε close to a i.e. in
(a−ε, a+ε). In other words for each ε there will be a number N (depending
on ε) such that when n > N, |a−an| < ε i.e. from N onwards the terms of
the sequence are ε close to a. Of course as we take smaller and smaller εs
more and more of the sequence will lie outside (a − ε, a + ε) but no matter
how small an ε it will always be only a finite number.
Example 1.3 In our area example, consider ε =
0.0001 then we see that
from n = 19 onwards we have | π −an| < ε. Remark that this does not prove
that an → π. In order to do that we would have to show that for any ε
we can find N (depending on ε of course) such that from n = N onwards
| π − an| < ε. We have only proved it for a single ε
Let’s formally prove that
1/n → 0, n → ∞.
Consider any ε > 0 and consider
1/ε
(if ε is very small this number will
be very large). Choose a large natural number N such that N >
1/ε
. Then
for any n > N we have n >
1/ε
and hence1/n
< ε. This proves that from N
onwards |1/n
− 0| =
1/n
< ε , which is precisely what it means for
1/n → 0.
Homework Problems (due Monday 10/6):
1. Show that for any two real numbers a, b the following inequality holds:
|a + b| ≤ |a| + |b| (Hint: consider separately the four cases a > 0, b > 0; a <
0, b > 0; a < 0, b < 0; a > 0, b < 0)
2. Show that for any two real numbers a, b, ||a| − |b|| ≤ |a − b|
3. Show that for any real number a the sequence a +
1/n → a
4. Show that if {an} and {bn} are sequences such that an → a and
bn → b then the sequence {an + bn} converges to a + b, and the sequence
{anbn} converges to ab



