Looking Forwards:
Why are the rules of arithmetic important
beyond high school mathematics ?
Content knowledge: Matrix arithmetic
Goal: Exploring why the rules of arithmetic are
important in linear algebra will deepen one's
perspective on the importance of the rules of
arithmetic.
Number Systems
There are some standard number systems:
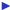
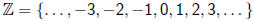
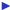Q = {p=q where p, q are integers and q ≠
0}
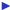R is the set of real numbers .
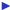C is the set of complex numbers .
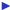There's many more!
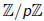or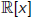 
and
so on.
These aren't just sets. I want to think of each as a set together
with some arithmetic operations . For simplicity , we'll just consider
+ and · (and ignore subtraction and division ).
Matrices
The system of 2 ·2 matrices is generalized number system. Here
are some examples of 2 ·2 matrices:
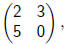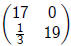or
, or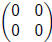 
A general 2 ·2 matrix can be written as follows:
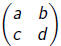
where a, b, c and d are real numbers.
Two matrices are equal if and only if every entry is
equal.
For instance:
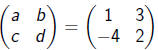
means that
a = 1, b = 3, c = -4 and d = 2
There are NO values of x such that the following equation
is
true:
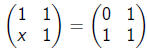
Adding matrices
You add matrices entrywise. For example:
Matrix addition can be summarized by the following
formula:
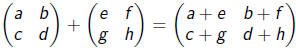
Matrix multiplication
Matrix multiplication can be summarized by the following
formula :
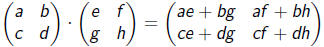
Motivating Question: What are the rules of
matrix arithmetic?
More specifically, which of the following statements are
true for all
2 ·2 matrices A, B and C:
1. (Commutative property of addition )
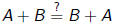
2. (Associative property of addition)
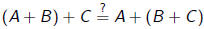
3. (Commutative property of multiplication)
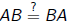
4. ( Distributive property )
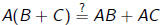
5. and so on . . .
Additive identity for numbers
If a is any number then:
a + 0 = a:
Additive Identity for Matrices?
True or False: If A is any 2 ·2 matrix, then:
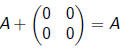
If true, explain why. If false, provide a counterexample.
Answer: True.
Moral: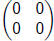 
is the additive identity for
the system of 2· 2
matrices.
Multiplicative Identity for Matrices?
True or False: If A is any 2 ·2 matrix, then:
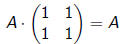
If true, explain why. If false, provide a counterexample.
Answer: False.
Multiplicative Identity for Matrices?
True or False: If A is any 2 ·2 matrix, then:
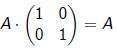
If true, explain why. If false, provide a counterexample.
Answer: True.
Moral: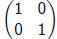
is the multiplicative identity
for the system of
2 ·2 matrices.
What are the other rules of matrix arithmetic?
