2001 Stanford Math Tournament
Algebra
1. Find the result of adding seven to the result of forty
divided by one -half.
2. Each valve A, B, and C, when open, releases water into
a tank at its own constant rate. With all three
valves open, the tank fills in 1 hour, with only valves A and C open it takes
1.5 hours, and with only
valves B and C open it takes 2 hours. How many hours will it take to fill the
tank with only valves A
and B open?
3. Julie has a 12 foot by 20 foot garden. She wants to put
fencing around it to keep out the neighbor’s
dog. Normal fenceposts cost $2 each while strong ones cost $3 each. If Julie
needs one fencepost for
every 2 feet and has $70 to spend on fenceposts, what is the greatest number of
strong fenceposts she
can buy?
4. p(x) is a real polynomial of degree at most 3. Suppose
there are four distinct solutions to the equation
p(x) = 7. What is p(0)?
5. Let f : N → N be defined by f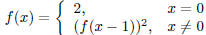
What is log 2f(11)?
6. If for three distinct positive numbers x, y, and z,
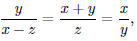
then find the numerical value of x/y .
7. If
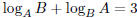and A < B, find
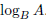
8. Determine the value of
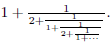
9. Find all solutions to (x − 3)(x − 1)(x + 3)(x + 5) = 13.
10. Suppose x, y, z satisfy
x + y + z = 3
x2 + y2 + z2 = 5
x3 + y3 + z3 = 7
Find x4 + y4 + z4.
2001 Stanford Math Tournament
Advanced Topics
1. Suppose
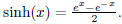What is the inverse function of sinh(x)?
2. Write
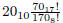as a decimal in base 6. The subscript indicates the base in which the
number is written
(i.e., 2010 is 20 base 10.)
3. There are 36 penguins in a row, and Barbara Manatee is standing in front of
them. In general, a
penguin rotation of penguins p1, p2, . . . , pn is a rearrangement of them such
that p1 moves to where
p2 was standing, and in general pi moves to where pi+1 was standing, and pn
moves to where p1
was standing. So, after a penguin rotation, the new order of these penguins is
pn, p1, p2, . . . , pn−1.
Whenever Barbara Manatee blows her whistle, the 2-4 penguins go through a
penguin rotation, the
5-9 penguins go through a penguin rotation, the 10-16 penguins go through a
penguin rotation, the
17-25 penguins go through a penguin rotation, and the 26-36 penguins go through
a penguin rotation.
What is the least positive number of whistle blows such that the penguins all
return to their original
position?
4. Eleven pirates find a treasure chest. When they split up the coins in it,
evenly among all the pirates,
they find that there are 5 coins left. They throw one pirate overboard and split
the coins again, only
to find that there are 3 coins left over. So, they throw another pirate over and
try again. This time,
the coins split perfectly. What is the least number of coins there could have
been?
5. Evaluate 1 · 2-1 + 3 · 2-2 + 5 · 2-3 + 7 · 2-4 + . . .
6. How many subsets of {n | n > 0 and n is a multiple of 3 less than 100} are
also subsets of {n | n > 0
and n is a multiple of 4 less than 100}?
7. There are 2000 dots spaced evenly around a circle. If 4 distinct dots A, B,
C, and D are picked
randomly, what is the probability that AB intersects CD?
8. Ashley, Bob, Carol, and Doug are rescued from a desert island by a pirate who
forces them to play a
game. Each of the four, in alphabetical order by their first names, is forced to
roll two dice . If the total
on the two dice is either 8 or 9, the person rolling the dice is forced to walk
the plank. The players go
in order until one player loses: A, B, C, D, A, B, .... What is the probability
that Doug survives?
9. There are 19 men numbered 1 though 19 and 20 women numbered 1 through 20
entered in a computer
dating service. The computer wants to match every man to a compatible woman, and
each man is
only compatible with women who have a number that is greater than equal to his
(i.e. man 19 is only
compatible with women 19 and 20, man 18 is only compatible with women 18, 19,
20, etc.). If each
women is matched with at most one man, let n be the number of ways that the
computer can match
them. What is the prime factorization of n ?
10. David is playing with Legos with velcro attached to the ends. He has green
Legos of length 1, blue
Legos of length 2, and red Legos of length 3, and wants to combine them (by
attaching them at the
ends) to make a “super-lego” of length 10. If any different ordering of colors
is considered a distinct
“super-lego”, how many ways can he make this “super-lego”?
2001 Stanford Math Tournament
Calculus
1. What is
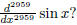
2. If f(x) = [x] is the greatest integer function, what is f'" (3.7)?
3. Suppose that f is a monotonically increasing continuous function defined on
the real numbers . We
know that f(0) = 0 and f(2) = 3. Let S be the set of all possible values of
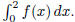What is the
least upper bound of S?
4. Evaluate
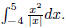
5.
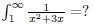
6. Given a point (p, q) on the ellipse
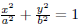where p
≠ 0, find the x- intercept of the tangent line at
(p, q) in terms of p, a, and b. (Note that a, b = 0.)
7. Find the number of real solutions to sin(6πx) = x, where x is in radians.
8. If a, b, and c are positive real numbers such that a + b + c = 16 and a2 + b2
+ c2 = 160, what is the
maximum possible value of abc?
9. For a given k > 0, n ≥ 2k > 0, consider the square R in the plane consisting
of all points (x, y) with
0 ≤ x, y ≤ n. Color each point in R gray if
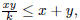and blue otherwise. Find the area of the gray
region in terms of n and k.
10. Let
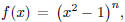where n is a positive integer. Determine, in terms of n, (a, b, c), where a,b,
and c are the number of distinct roots of
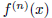in the intervals (−∞,−1), (−1,
1), and (1,+∞),
respectively.
2001 Stanford Math Tournament
Geometry
1. Find the coordinates of the points of intersection of the graphs of the
equations y = |2x| − 2 and
y = −|2x| + 2.
2. Jacques is building an igloo for his dog. The igloo’s inside and outside are
both perfectly hemispherical.
The interior height at the center is 2 feet. The igloo has no door yet and
contains
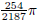cubic yards
of hand-packed snow. What is the circumference of the igloo at its base in feet?
3. Find the area of the convex quadrilateral whose vertices are (0, 0), (4, 5),
(9, 21), (−3, 7).
4. E is a point in the interior of rectangle ABCD. AB = 6, triangle ABE has area
6, and triangle CDE
has area 12. Find (EA)2 − (EB)2 + (EC)2 − (ED)2.
5. Two identical cones, each 2 inches in height, are held one directly above
another with the pointed end
facing down. The upper cone is completely filled with water. A small hole is
punctured in the bottom
of the upper cone so that the water trickles down into the bottom cone. When the
water reaches a
depth of 1 inch in the bottom cone, what is its depth in the upper cone?
6. Find the radius of a circle inscribed in the triangle determined by the lines
4x+3y = 24, 56x−33y =
−264, and 3x − 4y = 18.
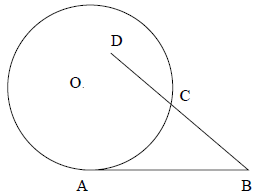
7. In the figure, AB is tangent at A to the circle with center O; point D is
interior to the circle; and DB
intersects the circle at C. If BC = DC = 3, OD = 2 and AB = 6, then find the
radius of the circle.
8. Let S be the solid tetrahedron with boundary points (0,
0, 0), (2, 4, 0), (5, 1, 0), (3, 2, 10). Let
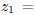
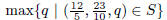and
let
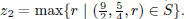Find
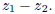
9. Circles A and B are tangent and have radii 1 and 2, respectively. A tangent
to circle A from the
point B intersects circle A at C. D is chosen on circle B so that AC is parallel
to BD and the two
segments BC and AD do not intersect. Segment AD intersects circle A at E. The
line through B and
E intersects circle A through another point F. Find EF.
10. E is a point inside square ABCD such that ∠ECD = ∠EDC = 15°. Find ∠AEB.
