Functions & First Degree Curves

Table of Contents

1. Functions & First Degree Curves
 1.1. Functions Revisited
• Is y a function of x? • Graphing • The Vertical Line Test
 1.2. Lines
• The Slope of a Line • The Two-Point Form • The Point-
Slope Form • The Slope- Intercept Form • The General Form
• Parallel & Perpendicular Lines

9. Functions & First Degree Curves

9.1. Functions Revisited

• Is y a function of x?
In everyday conversational speech we say that “something is a function
of something else.” For example, “success is a function of effort,”
“postage on a letter is a function of its weight,” “the diameter of a
tree is a function of its age,” and so on. These are statements assert
that a measure of one quantity, in some way, depends on the measure
of another quantity. However, in conversational speech, the exact way
in which one quantity depends on the other is not specified; indeed,
the exact relationship may be unknown. These are usually statements
of “feelings” or “relationships.”

In mathematics, we have the same type statements, “y is a function
of x,” but here, the meaning is precise.

We say that y is a function of x if we can find a function f(x) such
that
y = f(x).

There is no particular significance to the letters x and y; likewise, we
can say that x is a function of y provided there is some function g(y)
such that
x = g(y).

What does it mean for w to be a function of s? It means that the
variable w is expressible in terms of s:
w = h(s),

for some function h(s).

Illustration 1. Here are some examples of functions of different
variables.

(a) y = 4x^3 − 3x + 1 defines y as a function of x.
(b) x = 5y^4 − 8y + 12 defines x as a function of y.
(c) w = 2t + 1 defines w as a function of t.
(d) t = 1/2(w − 1) defines t as a function of w.
(e) A = πr^2 defines A, area, as a function of r, the radius of a circle.
(f) C = 2πr defines circumference of a circle, C, as a function of r,
the radius.
(g) r = C/2π defines radius, r, as a function of C.

Example 9.1. Given y = 3x − 1. Write x as a function of y.

Exercise 9.1. Respond to each of the following.
(a) Given y = 5x + 1, write x as a function of y.
(b) Given 4x − 2y = 1, write y as a function of x.
(c) Given 4x − 2y = 1, write x as a function of y.
(d) Given 2w + 3s^3 = 3, write s as a function of w.
(e) Given 2w + 3s^3 = 3, write w as a function of s.

In applications, you must create your own function of the appropriate
type.

Exercise 9.2. Suppose we have a cube and the total surface area is
known. The problem is to find the length of the common side of the
cube. Your assignment: Write the length, x, of the side of a cube as a
function of the surface area, S; i.e., write x = f(S). Use your formula
to compute the length of the common side of a cube having a total
surface area of 24 square units .

Exercise 9.3. Write the radius, r, of a sphere as a function of its
volume, V .

Exercise 9.4. Write the radius, r, of a sphere as a function of its
surface area, S.

Exercise 9.5. Solve each of the following: (a) A circle has a radius
of r = 3 units. Find the circumference, C, of the circle; (b) Another
circle has a circumference of C = 20π, find the radius, r, of this circle.
(Reference: Part (f) and Part (g) of Illustration 1.)

• Graphing
As you know, any equation in two variables, x and y, can be represented
as a curve in the plane . This curve is called the graph of the
equation.

We symbolically denote an equation by
F(x, y) = c (1)

where the left-hand side, F(x, y), represents some expression in two
variables , and the right-hand side c, is some constant. The graph of
(1) is the set of all points (x, y) in the plane that satisfy the equation.
(Sometimes we saythat the graph is the locus of all points that satisfy
the given equation.)

When we identifythe points on the graph of an equation, it is typically a
curve in the plane. The graph, then, is a visual and geometric
manifestation of the equation (1).

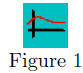
For example, consider the equation x^2/3 + y^2/3 = 2. The point
(1, 1) satisfies the equation since 1^2/3 + 1^2/3 = 2; in fact, all the
points (1, 1), (−1, 1), (1,−1) and (−1,−1) satisfy the equation.
These, though, are only four of infinitely many points. If we
identify enough points we can get a “feel” for the shape of the curve
and are thus able to draw it in. Figure 1 represents the graph of this
curve.

We shall not go into the technicalities of graphing; in the age of the
graphing calculator, many of the these age-old techniques seem antiquated.
Rather, we shall concentrate on study in this lesson, on the
properties of the straight line. In Lesson 10 we shall look at additional
curves: the parabola, the circle, and an introduction to the
circular (or trig) functions.

Some curves are the graphs of functions, others are not. The first
order of business is to classify curves as functional curves or not. In
the next section, we develop a basic, yet important, criteria for doing
exactly this.

• The Vertical Line Test
Curves that are graphs of functions are particularly important. Let
y = f(x) be a function. (In this case, we say that y is a function of
x.) We may look upon y = f(x) as an equation as discussed above.
(Rewrite y = f(x) as y−f(x) = 0, this makes is look like (1); however,
it is usually in convenient to write it this way.) The fact that y is a
function of x means that for any choice of x = x₀ in the domain of f,
there corresponds a unique y = y₀. This (x₀, y₀) pair will satisfy the
equation because that is the definition of a function: If y₀ corresponds
to x₀ with respect to the function f, then y₀ = f(x₀).

Now for the problem: Suppose you have a curve C drawn in the xy-plane.
How can we tell whether this curve C represents y as a function
of x?

There is a simple graphical test.

Vertical Line Test:
A curve C in the xy-plane defines y as a function of x if it is
true that every vertical line intersects the curve at no more
than one point.

Important. The x-axis is assumed to be the horizontal axis, and so
the meaning of vertical is perpendicular to the x-axis.

Exercise 9.6. Taking the definition of function into consideration,
the orientation of the axes (x-axis is horizontal), and the geometry of
the graph of a curve, justify in your own mind the Vertical Line Test.

The equation y = 2x + 1 defines y as a function x—here, f(x) =
2x + 1. Usually, we like the independent variable to be on the x-axis
(the horizontal axis); sometimes, however, things do not work out as
planned. The equation x = y^5 − y defines x as a function of y.

The concept of function is independent of the letters chosen to express
the relationship; here, in this instance, x = y^2 − y does define x as a
function of y—for each value of y there corresponds only one x. Now
the independent variable y is one the vertical axis and the dependent
variable is on the horizontal axis. I hope this does not disturb you
psychologically too much.

Exercise 9.7. When x is a function of y, x = g(y), and we graph the
equation in the xy-plane, what are the distinguishing characteristics
of the curve that determine it to be the graph of a function on y?

Given a curve in the plane we can discern whether it is a graph of a
function using the Vertical Line Test and its variant, the Horizontal
Line Test.

Quiz. Answer each of the following questions. Passing is 100%.

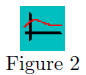
1. Does this curve define y a function of x?
(a) Yes (b) No

2. Does this curve define y a function of x?
(a) Yes (b) No

3. Does this curve define y a function of x?
(a) Yes (b) No

4. Does this curve define x a function of y?
(a) Yes (b) No

End Quiz.

9.2. Lines
Two points determine a line. We all know that. The problem is how
to express a line mathematically in a way we can manipulate it algebraically.

Let’s dispatch two simple cases first.

Vertical Lines: Let 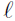be a vertical line. Characteristic of the points
on 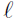is that they all have the same first coordinate. Let a be the x-intercept
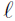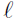of the line . Then an equation that describes the line is
given by

Thus, 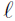is the set of all points that satisfy the above equation; i.e., all
points having an x-coordinate of a.

For example, the equation x = 3 is the vertical line that crosses the
x-axis at 3.

Horizontal Lines: Let 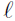be an horizontal line. Characteristic of the
points of 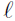is that they all have the same second coordinate. Let b be
the y-intercept of 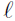the line , then the equation that describes the line
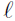is given by

y = b. (3)

The line 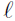consists of all points that satisfy the equation; i.e., all points
whose second coordinate is b.

For example, y = −4 is the horizontal line crossing the y-axis at −4.

For nonvertical lines, the analysis is not quite so simple. We begin by
a discussion of the slope of a line.

• The Slope of a Line
Let be a nonvertical line. Choose any two distinct points on ; call
them P(x₁, y₁) and Q(x₂, y₂). Then P and Q are not vertically oriented.

Question. What does it mean for P and Q not to be vertically oriented?

(a) x₁ = x₂ (b) x₁≠ y₂ (c) y₁ = y₂ (d) y₁ ≠ y₂

Slope of a Line:
Let 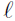be a nonvertical line and let P(x₁, y₁) and Q(x₂, y₂)
be any two points on this line. The slope, m, of the line is
given defined to be

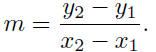
Comments: The value of the slope, m, does not depend on the two
points chosen to compute it. Indeed, if P(x₁, y₁) and Q(x₂, y₂)
are chosen from the line, and if 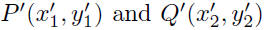are
another pair of points from the line, then by the principle of
similar triangles Figure 6, we have

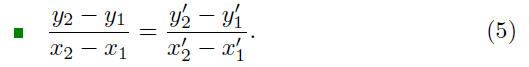
We compute the slope by taking the difference in the ordinates of the
two points and dividing by the difference in their abscissa—begin sure
to subtract in the same order.

Example 9.2. Calcuate the slope of the line that passes through
P(−1, 3) and Q(4, 1).

Exercise 9.8. Find the slope of the line passing through each of the
given pair of points.

(a) P(3, 1) and Q(4, 5) (b) P(−2,−3) and Q(0, 2)
(c) P(−1/2, 2/3) and Q(−3, 2) (d) P(2, 1) and the origin

• The Two-Point Form
Now let’s turn to the problem of creating an equation that describes
a line.

Given two points P(x₁, y₁) and Q(y₁, y₂). These two points determine
a unique line, namely the line passing through P and Q; call this line
. The slope of the line is given by

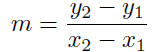
As was remarked earlier, the slope calculation does not depend on the
particular points on the line . If we take a generic point R(x, y) from
the line it should be true that

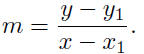
That is, m is also determined by the points R and P.

Now equate equations (6) and (7) to obtain

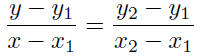
or,

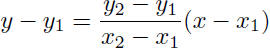
This last equation, called the two-point form of the equation of a line,
characterizes the points on the line .

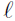Two-Point Form:
Let P(x₁, y₁) and Q(x₂, y₂) be two nonvertical points in the
plane. Then the equation of the line passing through these
two points is given by

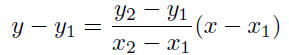
Example 9.3. Find the equation of the line passing through the two
points P(−2, 4) and Q(6, 9).

Having obtained the equation of a line, we can start to extract information
from it.

Example 9.4. For the line obtained in Example 9.3, find the y-intercept,
the x-intercept, and the points on the graph corresponding
to x = −3 and x = 6.

Exercise 9.9. Find the equation of the line passing through the two
points P(−4,−1) and Q(5, 1).

Exercise 9.10. Given the equation developed in the Exercise 9.9,
find the y-intercept and the x-intercept.

Exercise 9.11. Show that the equation for the line that crosses the
x-axis at x = 2 and the y-axis at y = 5 can be written in the form

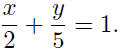
Exercise 9.12. (The Two-Intercept Form) Suppose a line crosses
the x-axis at x = a and the y-axis at y = b. Show that the equation
for this line can be written as

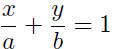
The two-intercept form can be a very quick way of writing down an
equation for a line if you know both intercepts.

Exercise 9.13. Write the equation of the line that crosses the x-axis
at x = 4 and the y-axis at y = −3.

• The Point-Slope Form
The two-point form was introduced above as a transitional form; i.e.,
you use it to establish an initial equation and then you manipulate
the equation to put it into a more useful form. The point-slope form
is the same way.

The Point-Slope Form:
Suppose it is known that a line has slope m and passes
through a point P(x₁, y₁). The equation of the line is given
by

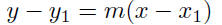
Example 9.5. Find the equation of the line with a slope of m = 5
and passes through the point P(1, 2). Leave the answer in the form
of y as a function of x.

Exercise 9.14. Find the equation of the line that passes through
the point P(3,−6) and having slope m = −2. Leave your answer in
the form of y as a function of x. Find another point on the line and
using these two points, make a sketch of the line.

Exercise 9.15. Find the equation of the line with a slope of m = −1/2
that passes through the point P(−2,−9). Leave your answer in the
form of x as a function of y.

• The Slope-Intercept Form
The slope-intercept form is one of the final forms of an equation of a
line, as opposed to a transitory form. The point-slope form is y−y1 =
m(x − y₁). As we did in the examples and exercises in the previous
paragraphs, we wrote this equation in the form of a function of x:

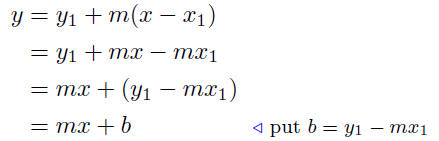
The equation y = mx + b is called the slope-intercept form of the
equation of a line. Of course, m is the slope of the line. But what
is the interpretation of the number b ? The y-intercept of a line is
obtained by putting x = 0 and solving for y. If we do that here we get

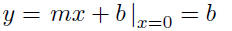
Thus, y = b is the y-intercept of the line.
Let’s record this in shadow box form.

Slope-Intercept Form:
The equation of the line 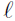having a slope of m and a y-intercept
of b given by
y = mx + b (11)

Exercise 9.16. Find the equation of the line that has slope 6 and
crosses the y-axis at −1.

Exercise 9.17. A line crosses the y-axis at y = 6 and has a slope of
m = −2. Find the equation of the line and leave your answer in the
form of a function of x.

Exercise 9.18. Find the equation of the line that passes through
the two points P(3, 1) and Q(4, 5). Leave your answer in the infamous
slope-intercept form, y = mx + b. (Reference: two-point form.)

Exercise 9.19. A line has slope m = 1/2 and passes through the point
P(−2,−5), find the equation of this line and leave your answer in the
slope-intercept form; i.e., leave your answer in the form of y as a
function of x. (Reference: The point-slope form.)

Quiz. Copy down the equation of the line described in Exercise 9.19
and use it to answer each of the following questions. Passing is 100%.

1. What is the y-intercept of this line?
(a) −8 (b) −4 (c) 4 (d) 8
2. Which of the following is the x-intercept of the line?
(a) −8 (b) −4 (c) 4 (d) 8
3. Is the point (2,−1) on this line?
(a) Yes (b) No
4. Write the equation for the line with x as a function of y:
(a) x = 2y + 8 (b) x = 2y − 8 (c) x = (1/2)y + 4 (d) x = (1/2)y − 4
5. Use the results of Question #4 to obtain the abscissa (the
x-coordinate) of the line when the line has an ordinate (a y-coordinate)
of 10.
(a) 1 (b) 10 (c) 14 (d) 28

EndQuiz.

This all seems all very simple. Given certain information, it is easy to
compute the equation of the line.

Exercise 9.20. Consider the two lines y = 3x − 1 and y = 1− x.
(a) Compute the slopes of each of these two lines
(b) State the y-intercepts of each line.

Exercise 9.21. The two lines in Exercise 9.20 intersect each other.
Find the point of intersection.

• The General Form
All the forms for the equation of a line can ultimately be written as
Ax + By + C = 0 (12)
This is called the General Form for the equation of a line.

For example, in Exercise 9.19 we obtained the equation for a line
as y = (1/2)x − 4, written in the slope-intercept form. After a few algebraic
steps, we obtain x − 2y − 8 = 0, which is in the same form as
equation (12).

The General Form, like many of the forms, is not unique. For example,
we can write x−2y−8 = 0 as (1/2)x−y−4 = 0, or as 3x−6y−24 = 0.
Usually though, we are true to our algebraic roots and remove any
common factors (so 3x−6y −24 = 0 is not considered “good form”);
and if the coefficients are all rational numbers , we usually clear fractions
and write the equation with integer coefficients (so (1/2)x−y−4 = 0
is not a preferred form).

We can also put the constant term to the other side of the equation;
thus, x − 2y = 8 would be considered in the General Form of the
equation of a line.

Example 9.6. Calculate the slope of the line 2x − 3y = 5.

Exercise 9.22. Find the slope and y-intercept of each of the following
equations.
(a) 5x + 3y − 1 = 0 (b) −3x + 12y+13 = 0 (c) x − y = 0

Exercise 9.23. Sketch the graph of each line in Exercise 9.22 by
plotting the y -intercept and by finding and plotting an additional
point.

Exercise 9.24. Find the equation of the line that passes through the
points (−4, 1) and (5, 1). Leave your answer in the General Form.

Recall, the y-intercept is obtained by putting x = 0 and solving for
y, and the x-intercept is obtained by putting y = 0 and solving for x.
Use these simple criteria to solve the next problem.

Exercise 9.25. Find the x- and y-intercepts of each of the lines,
and sketch their graphs by plotting the intercepts and drawing a line
through them.

(a) 3x + 4y = 24 (b) 5x − 2y = 10 (c) x − 2y = 1

Exercise 9.26. Find the points of intersection between the following
pairs of lines. (Warning: In one of the parts below, the lines do not
intersect.) Leave your answer should be a point in the plane: P(a, b).
(a) x − y = 1 and x + y = 1
(b) x − 3y = 1 and 2x − y = 1
(c) 4x − 2y = 7 and y = 2x + 1
(d) 6x + y = 3 and x + y = 2

• Parallel & Perpendicular Lines
The last topic under consideration in this lesson is to develop criteria
for determining whether two lines are parallel or perpendicular.

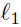Parallel Lines: Two lines and 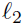are parallel if and only if they do
not intersect. Suppose the equations of these lines are y = m₁x + b₁
and y = m₂x + b₂, respectively. When we try to find the point of
intersection we equate

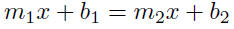
and try to solve for x:

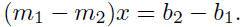
We can divide by m₁−m₂ to get the solution for x, provided m₁−m₂ ≠
0. It is the singular case of m₁ −m₂ = 0 in which we cannot solve for
x; this is the case in which the lines are parallel.

Parallel Lines:
Two lines 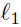and 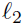having slopes m₁ and m₂ respectively,
are parallel if and only if
m₁ = m₂ (13)
that is, if and only if they have the same slope.

When the lines are written as functions of x, i.e., in the slope-intercept
form, it is trivial to see whether the lines are parallel. For example,
y = 2x−5 and y = 2x+12 are parallel because the slope of each line
is m = 2. The two lines y = 3x − 4 and y = 5x + 1 are not parallel
because the first line has slope m₁ = 3 and the second line has slope
m₂ = 5.

When the lines are in general form some slight effort is needed to
determine whether two lines are parallel—simply put the equations
in the infamous slope-intercept form, at which point you can make an
easy determination.

Quiz. Which of the following pairs of lines are parallel. Passing is
100%.
1. Are the lines x + 2y + 3 = 0 and 3x + 6y + 1 = 0 parallel?
(a) Yes (b) No
2. Are the lines 3y − 2x = 3 and 12y − x = 6 parallel?
(a) Yes (b) No
3. Are the lines 5x − 2y = 1 and 4y − 10x = 2 parallel?
(a) Yes (b) No

End Quiz.

Exercise 9.27. Find the equation of the line that is parallel to the
line y = 2x − 1 but passes through the point P(2, 7).

Exercise 9.28. Find the equation of the line that passes through
the point P(−3,−1) and is parallel to the line 5x + 4y = 12.

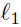Parallel Lines: Two lines and 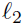  are perpendicular or
orthogonal if they intersect and at the point of intersection the angle
between the two lines is 90º.We state the following criteria with proof.

Perpendicular Lines:
Let 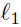be a line with slope m₁ ≠ 0 and 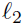be a line with
slope m₂ ≠ 0, then 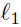is perpendicular to 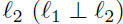if and
only if
m₁ · m₂ = −1 or m₂ = − 1/m₂
, (14)
that is, if and only if the slope of one line is the negative
reciprocal of the other .

Exercise 9.29. Think about the cases excluded explicitly in the criteria
for perpendicular lines. When are lines that fall into the exceptional
case perpendicular?

Quiz. Which of the following pairs of lines are perpendicular to each
other. Passing is 100%.
1. Are the lines y = 2x + 1 and y = −(1/2)x − 3 perpendicular?
(a) Yes (b) No
2. Are the lines x − 3y + 3 = 0 and 3x + y − 2 = 0 perpendicular?
(a) Yes (b) No
3. Are the lines 3x − 6y = 1 and 9x + 3y = 2 perpendicular?
(a) Yes (b) No

EndQuiz.

Exercise 9.30. Find the equation of the line that passes through
the point P(3, 4) and is perpendicular to the line y = 5x + 1.

Exercise 9.31. Find the equation of the line that passes through
the point P(−5, 3) and is perpendicular to the line 6x + 2y = 1.

We have now developed enough tools to successfullytac kle the following
problem.

Exercise 9.32. Find the distance the point P(−1,−1) is away from
the line y = 2x + 4. Answer this question byfirst mapping out a
strategy, then carrying out your strategy.Parts (a) and (b) correspond
to each of these two steps.
(a) Plot the point and the line, then map out in a series of steps
how you plan to solve this problem.
(b) Now carryout your game plan.

We have come to the end of Lesson 9. Lesson 10 continues the discussion
of some common, yet important curves: parabolas, circles, and
trig functions.