Introduction to Maple (Math 502) Assignments

Thu., May. 8:
Final Examination: 4:00 { 6:00
Blog of last minute questions (PDF for printing |classical HTML for terminal
window browsing)
Note: this page may have changed since the last time you looked at it. Therefore, reload
it each time you look at it.

Wed., May. 7:
O ce hours: 3:00 { 5:00

Tue., May. 6:
Last regular class meeting. Bring questions for review.

Thu., May. 1:
Written Assignment No. 5 (PDF for printing |classical HTML for terminal win-
dow browsing) is due.

Tue., April. 29:
1. Convert the word "sage" to its vector of ASCII codes and then use El Gamal en-
cryption for multiplicative arithmetic modulo the prime 257 to encrypt these values
using the formula

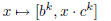(mod 257)

where b = 102 and c = 150 employing for the 4 characters the 4 successive values
k = 11, 12, 13, 14.

2. How can the word "sage" be recovered from the four pairs of values modulo 257 that
were obtained in the preceding exercise ?

Added after the class : Solution of Exercise 3 (PDF for printing |classical HTML9 for
terminal window browsing).

Thu., April. 24:
Do these these exercises (PDF for printing |classical HTML for terminal window
browsing).

Tues., Apr. 22:
Read: § 10.5, 10.6
224: 3 - 5
260: 3 - 5
And this:
For the cubic curve y² = x³ - 43x + 166:

(a) Find a point with rational coordinates that has order 7.
(b) How many points lie on this curve in the field Z/41Z?
(c) Find examples of points on the curve in the field Z/41Z having the orders
2, 3, 6, 7, 14, 21, and 42.

Thu., April. 17:
Written Assignment No. 4 (PDF for printing |classical HTML for terminal
window browsing) is due.

Tue., April. 15:
Become familiar with the functions for cubic curves found at the course's code archive,

Use this introduction (PDF for printing - classical HTML for terminal window
browsing) as a beginning guide.

Thu., April. 10:
Study the slides (also available as PDF or DVI or classical HTML) about addition of
points on cubic curves.

Tue., Apr. 8:
Read: § 10.1 - 10.2
260: 1, 2
And this: Find the area enclosed by the loop of the cubic curve y² = x³ - x.
Repeat for the cubic curve y² = x - x³.

Thu., Apr. 3:
Written Assignment No. 3 (PDF for printing |classical HTML for terminal
window browsing) is due.

Tue., Apr. 1:
Read: § 9.1 - 9.2
224: 1, 2
And this: Find the polynomials 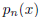such that

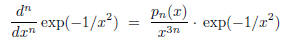
for 1 ≤ n ≤ 7. Can you give a general recursive formula for ?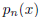

Tue., Thu., Mar. 25, 27:
No classes: university recess.

Thu., Mar. 20:
Read: § 7.4 - 7.6, 8.6 - 8.8
1. Do these: 188: 3, 4, 5
2. Explore the Maple function for finding primitive roots mod m, which is numtheory [primroot].

a. Find the smallest primitive root modulo 289 that is larger than 100.
b. Find the smallest positive non -prime primitive root mod 40487.
c. Find the smallest positive number that is primitive modulo both 101 and
103. Is it primitive mod 101 * 103?
d. If c is primitive modulo both 101 and 103, what congruence condition on
integers j, k ≥ 0 is equivalent to the condition that 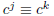(mod 101 * 103)?

3. Let p be the prime 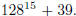  Without trying to solve determine which of the
following two congruence equations is solvable :

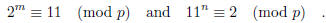
Are you able to solve the solvable one?

Tue., Mar. 18:
Read: § 7.1 -  7.3
174: 5
188: 1, 2
And this: Continuing in the context of the last exercise in the previous assignment,
you are now being told that the squeezed vector

[712147006187606979338143444233878549915653153140991743218564586,
1786621100356707079804781015651798041041290004401049203827247506,
1782184643903441535885937756067735301974983951149305281678962346,
1639000008839632707546680167815675641387259213687418193657940006,
1535960089185549654706004534787094483505037489361312984436350635,
1195799297844909964188410557114692983427064185633447219054911622,
1529236902471918734371483225353942522875473990416411009757742702,
409979669999633360347425246927425729369778446996539051720679885,
1805600608974788719838347443426498779266916648865325622675849897,
1058983644708927766918309320955981103594250701210512127725439642]

(where k is maximum, as before, for the given modulus m) may be decrypted with
the exponent

d = 679417638057246102387290084428241348920601574129013039486178441 :

A. Decrypt it, expand its terms in base 128, and convert the resulting vector,
regarded as a sequence of ASCII codes, to a string.
B. Can you determine what the encrypting exponent was?

Thu., Mar. 13:
Read:  § 6.1 - 6.3
174: 1 { 3, disregard the last sentence in exercise 1.
And this: Given a vector of digits in base 128 what is the largest block size k
for squeezing the vector into a vector of digits for base 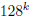so that the resulting
squeezed vector can be faithfully encrypted by taking a suitable power of each entry
modulo the integer

m = 2468256835981809063232453773840873253369376547681693188080273739

under the hypothesis, which is satisfied here, that the integer m is square -free?