Midterm Details
The third exam will cover Sections 5.1-5.4.
•For those classes meeting on Mondays and Wednesdays, the exam will be on
Monday,
November 17.
•For those classes meeting on Tuesdays and Thursdays, the exam will be on
Thursday,
November 18.
•The review session for Exam II will be on Thursday, November 13 at 6:30-7:30 PM
in
Nursing and Math 357. You can download a copy of the slides for the review
session
at the Exams page of the Math 127 Course Website.
You will be permitted one 4 *6-inch note card; however, Calculators will not be
allowed on
this exam. For those students qualifying for special accommodations, please send
a reminder
email no later than Wednesday, November 12.
Studying and Reviewing
•You should try working problems in the review sections at the end of Chapter 5
(pp.
360-362).
•Be sure to take advantage of the office hours and the
AARC.
Topics for Exam III
•To understand and to be able to apply the definition a rational number (Section
5.1).
•To understand when two fractions are equivalent and to be able to simplify
fractions
(Section 5.1).
•To understand that the rational numbers are ordered and can be placed into a
one-to-
one correspondence with the natural numbers (Section 5.1).
•To understand that given any two rational numbers, we can find a rational
number
between these two numbers (Section 5.1).
•To understand and to be able to add and subtract rational numbers (Section
5.2).
•To understand and be able to use fractions and mixed numbers (Section 5.2).
•To be able to estimate with rational numbers (Section 5.2).
•To understand and to be able to multiply and divide rational numbers (Section
5.3).
•To understand and be able to use fractions and mixed numbers (Section 5.3).
•To be able to estimate with rational numbers (Section 5.3).
•To understand and to be able to apply proportional reasoning . If a, b ≠ 0, c,
and d≠ 0
are real numbers , then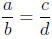 if and only if ad = bc
(Section 5.4).
if and only if ad = bc
(Section 5.4).
•A quantity x is said to be proportional to a quantity y if y = kx. In this
case, k is the
constant of proportionality (Section 5.4).