Abstract
1 Divisibility
• Take questions and review some concepts from homework.
• Theorem ( Division algorithm ): If a, b ∈ Z and a ≠ 0, there exist unique
integers, q and
r, such that b = qa + r, where 0 ≤ r < |a|, or
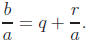
Proof: Note that a = sgn(a)|a|, so we can consider the
case of a and b both positive.
The quotient is how many times a may be subtracted from b before b becomes
negative.
That is, q is largest integer n such that b - na is nonnegative; then r = b - qa.
– Let S = {b- na | n ∈ Z and b - na ≥ 0. Note that if b ≥ 0, then b - 0a = b ∈
S,
so S is not empty.
– Call r the smallest element of S. Note that r < |a|, since if r ≥ a, then 0 ≤
r - a = b - qa - a = b - (q + 1)a ∈ S, contrary to the assumption that r is the
smallest member of S.
– Uniqueness: Suppose that b = aq + r = aq' + r', where 0 ≤ r, r' < a. Then
r = b - aq and r' = b - aq' are both in S. Since elements of S differ by
multiples
of a, only one member lies in [0, a). Because r and r' both fall in this
interval, we
have r = r'. Then b - aq = b - aq', whence q = q'.
• Let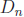 
be the set of divisors of n , and let
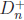be the set of positive divisors of n.
• Definition: A natural number p > 1 is prime if the only
positive divisors of p are 1 and
p; that is, if 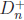= {1, p}. Note that 1 is
not prime.
• The set of prime numbers is often denoted by P.
• The set of natural numbers n > 1 that are not prime are called composite.
• The set of composite numbers is often denoted by C. Then N = {1} ∪ P ∪ C.
• Any composite number n can be written as a product of other numbers
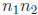, each
of which may be prime or composite. Recurse until you have a product of primes,
so: Theorem: Any natural number > 1 can be factored as a product of primes, n =
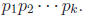
• Theorem: There are infinitely many prime numbers. Proof (Euclid): Suppose, to
the
contrary, that there is a largest prime number, so there are only a finite set
of them,
{
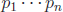. The number
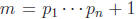is then not divisible by any of them, etc.
Note that this does not mean that 2 · 3 · 5 · 7 · 11· 13 + 1 = 30031 = 59 · 509
is prime!
(Also note that the prime factors of 30031 are both greater than 13.)
• Example: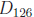 
=
{±1,±2,±3,±6,±7,±9,±14,±18,±21,±42,±63,±126}
• Example: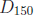 
=
{±1,±2,±3,±5,±6,±10,±15,±25,±30,±50,±75,±150}
• Note that ∩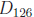
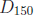= {±1,±2,±3,±6} is the set of numbers that
simultaneously
divide 126 and 150. The set has a greatest element , namely 6, called the
greatest
common divisor of 126 and 150.
• Definition: Given integers m and n, not both zero , the greatest common divisor
(GCD)
of m and n, denoted by gcd(m, n), is the natural number d such that
– d|m and d|n, and
– u|m and u|n => d ≥ u.
• Example: To compute gcd(m, 0), note that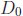 
=
Z\{0}, so ∩ 
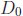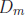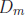= . The
greatest element of 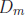is |m|, so gcd(0,m) =
|m|.
• Definition: Two integers m and n, not both zero, are relatively prime if gcd(m,
n) = 1.
That is, m and n are relatively prime if they have no common factors other than
±1.
Note that two numbers do not need to be prime in order to be relatively prime;
for
example, 14 and 15 are relatively prime, even though neither is prime.
• Note that the definition of gcd and of relatively prime can be extended to
more than
two numbers. For example, gcd(30, 42, 66) is the maximum number in the set
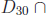
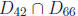, which is 6. Moreover, the numbers 30, 42
and 66 are not relatively prime,
but the numbers 30, 42 and 65 are relatively prime because
.
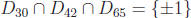• The least common multiple (LCM) of m and n, not both
zero, is the smallest positive
integer that is a multiple of both m and n. It is denoted by lcm (m, n). We know
that
mn is a multiple of both m and n, so lcm (m, n) ≤ mn, which shows that lcm(m, n)
always exists.
