INTERMEDIATE ALGEBRA

VIII. COURSE OUTLINE

A. Unit One: Chapter Six Rational Expressions
1. Unit Objectives: Upon successful completion of this unit the student will be able to do the following:
 a. Find the domain of a rational expression
 b. Simplify rational expressions
 c. Multiply rational expressions
 d. Divide rational expressions
 e. Use rational functions in applications
 f. Add or subtract rational expressions with common denominators
 g. Identify the least common denominator of two or more rational expressions
 h. Add or subtract rational expressions with unlike denominators
 i. Simplify complex fractions by simplifying the numerator and denominator and then dividing
 j. Simplify complex fractions by multiplying by a common denominator
 k. Simplify expressions with negative exponents
 l. Divide a polynomial by a monomial
 m. Divide by a polynomial
 n. Use synthetic division to divide a polynomial by a binomial
 o. Use the remainder theorem to evaluate polynomials
 p. Solve equations containing rational expressions
 q. Solve an equation containing rational expressions for a specified variable
 r. Solve problems by writing equations containing rational expressions
 s. Solve problems involving direct variation
 t. Solve problems involving inverse variation
 u. Solve problems involving joint variation
 v. Solve problems involving combined variation

2. Learning Activities:
 a. Classroom lecture/discussion (F5, F6, F7, F8)
 b. Reading/homework assignments (F1, F2, F7, F8, F9, F10, F11, F12)

3. Unit Outline:
 a. Section 6.1 Rational Functions and Multiplying and Dividing Rational Expressions
 b. Section 6.2 Adding and Subtracting Rational Expressions
 c. Section 6.3 Simplifying Complex Fractions
 d. Section 6.4 Dividing Polynomials: Long Division and Synthetic
Division
 e. Section 6.5 Solving Equations Containing Rational Expressions
 f. Section 6.6 Rational Equations and Problem Solving
 g. Section 6.7 Variation and Problem Solving

B. Unit Two: Chapter Seven Rational Exponents, Radicals, and Complex Numbers
 1. Unit Objectives: Upon successful completion of this unit the student will be able to do the following:
 a. Find square roots
 b. Approximate roots
 c. Find cube roots
 d. Find nth roots
 e. Find 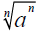where is a real number a
 f. Graph square and cube root functions
 g. Understand the meaning of
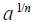
 h. Understand the meaning of
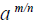
 i. Understand the meaning of
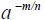
 j. Use rules for exponents to simplify expressions that contain rational exponents
 k. Use rational exponents to simplify radical expressions
 l. Use the product rule for radicals
 m. Use the quotient rule for radicals
 n. Simplify radicals
 o. Use the distance and midpoint formula
 p. Add or subtract radical expressions
 q. Multiply radical expressions
 r. Rationalize denominators
 s. Rationalize denominators having two terms
 t. Rationalize numerators
 u. Solve equations that contain radical expressions
 v. Use the Pythagorean Theorem to model problems
 w. Write square roots of negative numbers in the form bi
 x. Add or subtract complex numbers
 y. Multiply complex numbers
 z. Divide complex numbers
 aa. Raise i to powers

2. Learning Activities:
 a. Classroom lecture/discussion (F5, F6, F7, F8)
 b. Reading/homework assignments (F1, F2, F7, F8, F9, F10, F11, F12)

3. Unit Outline:
 a. Section 7.1 Radicals and Radical Functions
 b. Section 7.2 Rational Exponents
 c. Section 7.3 Simplifying Radical Expressions
 d. Section 7.4 Adding, Subtracting and Multiplying Radical Expressions
 e. Section 7.5 Rationalizing Denominators and Numerators of Radical Expressions
 f. Section 7.6 Radical Equations and Problem Solving
 g. Section 7.7 Complex Numbers

C. Unit Three: Nonlinear Systems, Functions and their Graphs
1. Unit Objectives: Upon successful completion of this unit the student will be able to do the following:
 a. Solve a nonlinear system by substitution
 b. Solve a nonlinear system by elimination
 c. Define relation, domain, and range
 d. Identify functions
 e. Use the vertical line test for functions
 f. Find the domain and range of a function
 g. Use function notation
 h. Add, subtract, multiply, and divide functions
 i. Construct composite functions
 j. Graph piecewise-defined functions
 k. Vertical and horizontal shifts
 l. Reflect graphs
 m. Stretch and compress graphs of absolute value functions

2. Learning Activities:
 a. Classroom lecture/discussion (F5, F6, F7, F8)
 b. Reading/homework assignments (F1, F2, F7, F8, F9, F10, F11, F12)

3. Unit Outline:
 a. Section 10.3 Solving Nonlinear Systems of Equations
 b. Section 3.2 Introduction to Functions
 c. Section 9.1 The Algebra of Functions; Composite Functions
 d. Section 3.6 Graphing Piecewise-Defined Functions and Shifting and Reflecting Graphs of Functions
 e. Appendix C Stretching and Compressing Graphs of Absolute Value Functions

D. Unit Four: Chapter Eight Quadratic Equations and Functions
1. Unit Objectives: Upon successful completion of this unit the student will be able to do the following:
 a. Use the square root property to solve quadratic equations
 b. Solve quadratic equations by completing the square
 c. Use quadratic equations to solve problems
 d. Solve quadratic equations by using the quadratic formula
 e. Determine the number and type of solutions of a quadratic equation by using the discriminant
 f. Solve geometric problems modeled by quadratic equations
 g. Solve various equations that are quadratic in form
 h. Solve problems that lead to quadratic equations
 i. Solve polynomial inequalities of degree 2 or greater
 j. Solve inequalities that contain rational expressions with variables in the denominator
 k. Graph quadratic functions of the form f(x) = x² + k
 l. Graph quadratic functions of the form f(x) = (x - h)²
 m. Graph quadratic functions of the form f(x) = (x - h)² + k
 n. Graph quadratic functions of the form f(x) = ax²
 o. Graph quadratic functions of the form f(x) = a(x – h)² + k
 p. Write quadratic functions of the form y = a(x – h)² + k
 q. Derive a formula for finding the vertex of a parabola
 r. Find the minimum or maximum value of a quadratic function

2. Learning Activities:
 a. Classroom lecture/discussion (F5, F6, F7, F8)
 b. Reading/homework assignments (F1, F2, F7, F8, F9, F10, F11, F12)

3. Unit Outline:
 a. Section 8.1 Solving Quadratic Equations by Completing the Square
 b. Section 8.2 Solving Quadratic Equations by the Quadratic Formula
 c. Section 8.3 Solving Equations by Using Quadratic Methods
 d. Section 8.4 Nonlinear Inequalities in One Variable
 e. Section 8.5 Quadratic Functions and Their Graphs
 f. Section 8.6 Further Graphing of Quadratic Functions

E. Unit Five: Chapter Nine Exponential and Logarithmic Functions
1. Unit Objectives: Upon successful completion of this unit the student will be able to do the following:
 a. Determine whether a function is a one-to-one function
 b. Use the horizontal line test to decide whether a function is a one-to-one function
 c. Find the inverse of a function
 d. Find the equation of the inverse of a function
 e. Graph functions and their inverses
 f. Determine whether two functions are inverses of each other
 g. Graph exponential functions
 h. Solve equations of the form bx = by
 i. Solve problems modeled by exponential equations
 j. Write exponential equations with logarithmic notation and write logarithmic equations with exponential notation
 k. Solve logarithmic equations by using exponential notation
 l. Identify and graph logarithmic functions
 m. Use the product property of logarithms
 n. Use the quotient property of logarithms
 o. Use the power property of logarithms
 p. Use the properties of logarithms together
 q. Identify common logarithms and approximate them by calculator
 r. Evaluate common logarithms of powers of 10
 s. Identify natural logarithms and approximate them by calculator
 t. Evaluate natural logarithms of powers of e
 u. Use the change of base formula
 v. Solve exponential equations
 w. Solve logarithmic equations
 x. Solve problems that can be modeled by exponential and logarithmic equations

2. Learning Activities:
 a. Classroom lecture/discussion (F5, F6, F7, F8)
 b. Reading/homework assignments (F1, F2, F7, F8, F9, F10, F11, F12)

3. Unit Outline:
 a. Section 9.2 Inverse Functions
 b. Section 9.3 Exponential Functions
 c. Section 9.4 Logarithmic Functions
 d. Section 9.5 Properties of Logarithms
 e. Section 9.6 Common Logarithms, Natural Logarithms, and Change of Base
 f. Section 9.7 Exponential and Logarithmic Equations and Applications