GOAL: Understand the concept of slope for lines and
linear functions and learn how to visualize
quadratic functions by completing the square.
► A linear function is a function of the form
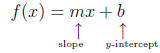where
m and b are given numbers
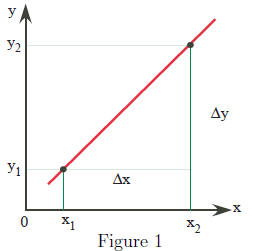
• Slope = m =
Exercise 1 Find the slope of the line passing through (−1, 1) and
(2, 7).
• Equation of line passing through a point (x1, y1) and with a given slope
m:
If (x, y) is another point on the line then
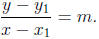So we have
point- slope form :
Exercise 2 Find the equation of the line through
(−1, 1) and with slope 2.
Exercise 3 A small surf shop has fixed expenses of
$850 per month. Each surfboard costs $100 to
make and sells for $550.
(a) Write the monthly cost, revenue, and profit as
functions of the number of surfboards made.
Cost function = C(x)
Revenue function = R(x)
Profit function = P(x)
(b) Find the break-even point.
Ans. x ≈ 2
Exercise 4 The demand curve of bread in a bakery
shop is q = D(p) = −50(p − 5) and its supply
curve is q = S(p) = 50(p − 1), where the price p is in dollars and the quantity
q is in loaves. Find the
equilibrium price pe and equilibrium quantity qe.
Ans. pe = 3, qe = 100
► A quadratic function is a function of the form f(x) =
ax2 + bx + c, where a ≠ 0, b and c are
given numbers . It always can be written in the informative form f(x) = a(x −
h)2 + k, which is a
horizontal translation by h and a vertical translation by k of the simple
parabola f(x) = ax2.
Exercise 5 Consider the quadratic function f(x) =
−x2 + 6x − 5.
(i) Complete the square to write it in the form f(x) = a(x − h)2 + k.
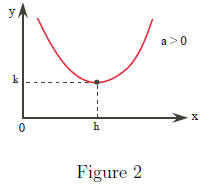
(ii) Use (i) to decide whether f(x) has a minimum value or a maximum value and
where it is taken.
(iii) Use (i) to find the roots of f (x).
(iv) Determine the axis of symmetry and the y- intercept and sketch the graph of
f(x).
Exercise 6 A furniture company making oak desks has
a fixed cost of $5, 000 per month and a cost
per desk of $500. Find how many desks per month it should produce to maximize
its profit if the price
is given by p = 1000 − 2.5x, where x denotes the number of oak desks produced by
the company.
Ans. x = 100
Exercise 7 Consider the quadtratic f(x) = x2 − 5x
+ 4.
(a) Find its zeros using the quadratic formula :
(b) Factor it .
(c) Determine its sign .
