Example
10.17 [Repeated Real Characteristic Roots]
Solve and graph the solution of the IVP
Solution: The characteristic equation is
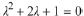
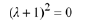
with the repeated real roots
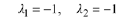
Theorem 10.9 shows that a general solution is given by
Next, calculate values of
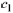and 
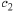to satisfy the initial conditions. Set
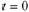in Eqn
(10.11):
Now, differentiate Eqn . (10.11) with respect to
and set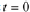 
in Eqn. (10.13):
Solve Eqs (10.12) and (10.14) for
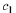and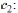 
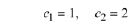
So the solution to the IVP is
End
of Example 10.17
Case 3: Complex Conjugate Characteristic Roots - 3 Examples
Example
10.18 [Complex Conjugate Characteristic Roots - Real part Zero ]
Solve the IVP
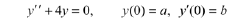
for arbitrary parameters a and b Then plot the three solutions that correspond to
the following sets of values for a and b .
and plot the results.
Solution: The characteristic equation is
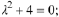it factors as
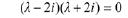
to get the complex conjugate roots (with real part zero)
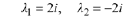
Theorem 10.9 shows that a general solution is given by
We calculate values of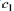 
and
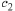to satisfy the initial conditions
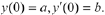Differentiate Eqn.
(10.16) to obtain
Eqn. (10.16) and (10.17) imply that
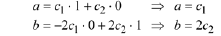
Hence the solution to the IVP is
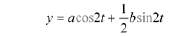
The calculations of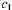 
and
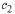for each of the three sets of initial conditions are
left to the reader. Note that all three IC's have the same value
for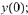 
they just differ in the values for
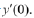We get
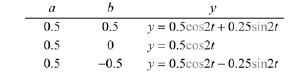
Also observe that all solutions as well as the general solution are periodic
with period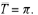 
End
of Example 10.18
Example
10.19 [Complex Conjugate Characteristic Roots - Real Part Positive ]
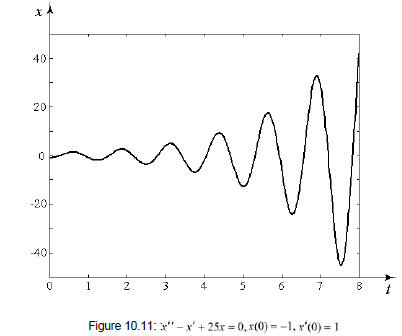
Solve and graph the solution of the IVP
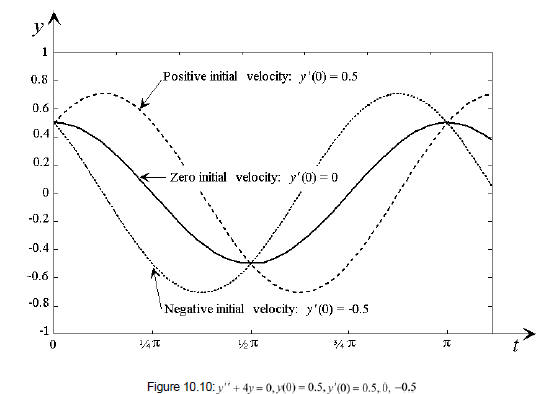
Solution: The characteristic equation is
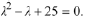As this polynomial doesn 't factor
readily, use the quadratic formula to calculate the
characteristic roots
Theorem 10.9 shows that a general solution is given by
Next, calculate values of
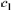and 
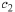to satisfy the initial conditions. Set
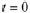in Eqn
(10.18):
Differentiate Eqn (10.18): with respect to
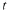
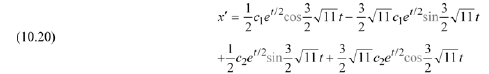
and set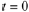 
in Eqn. (10.20):
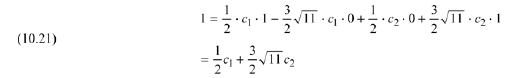
Use Eqn. (10.19) to solve Eqn. (10.21) for
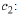
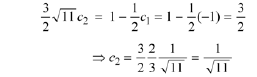
So the solution to the IVP is
and with a plot in Figure 10.11.
End
of Example 10.19
Example
10.20 [Complex Conjugate Characteristic Roots - Real Part Negative ]
Solve and graph the solution of the IVP
Solution: The ODE is similar to Example 14.15 The characteristic equation is
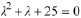with characteristic roots
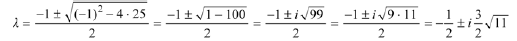
Set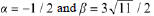 
(the real and imaginary parts of
λ ). Then Theorem 10.6 shows that a
general solution is given by
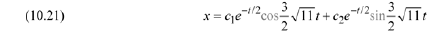
Next, calculate values of
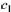and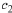 
to satisfy the initial conditions. Set
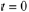in Eqn.
(10.21):
Differentiate Eqn. (10.21) with respect to
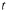
and set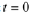 
in Eqn. (10.23):
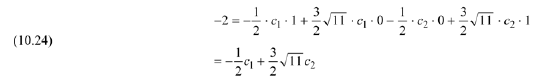
Use Eqn. (10.22) to solve Eqn. (10.24) for
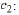
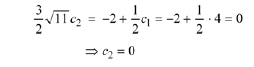
So the solution to the IVP is
and with its graph sketched in Figure 10.12
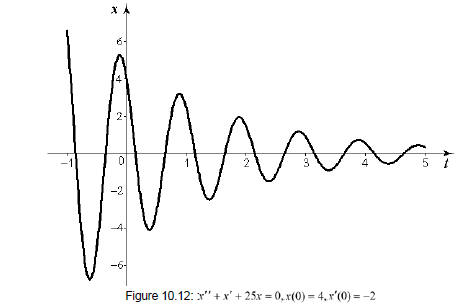
End
of Example 10.20
