Be sure to explain how you obtain your answers!!
1. Here is a data table showing how fast ants run at
various air temperatures:
| Temperature |
25.6 |
27.5 |
30.3 |
30.4 |
| Speed |
2.62 |
3.03 |
3.52 |
3.56 |
Here temperature is in degrees Celsius and speed is in
centimeters per second.
(a) Find the equation of the regression line of speed as a
linear function of temperature.
(b) Plot on this paper the data points and the regression line.
(c) What aspect of the plot in Part (b) shows that the data is not precisely
linear?
(d) What aspect of the plot in Part (b) shows that the data can be approximated
well
by a linear function ?
(e) Determine the slope of the regression line; be sure to indicate the units
for the slope.
(f) According to the linear regression model, how fast will ants run at zero
degrees
Celsius? Comment on this.
2. The temperature of a potato placed in a preheated oven
is given by
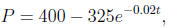
where P is degrees Fahrenheit and t is minutes since the
potato was placed in the oven.
(a) Graph P as a function of t for values of t up to 120 minutes.
(b) The potato is cooked when it reaches 270 degrees. When will the potato be
done?
(c) What is the initial temperature of the potato?
(d) Did the potato’s temperature rise more in the first thirty minutes or the
second thiry
minutes?
(e) What is the concavity of the graph of P (concave up or concave down) ?
Explain
what this means in terms of the temperature of the potato.
(f) Sketch a graph of dP/dt as a function of t.
(g) Explain how your graph in (f) is related to the concavity of the graph of P.
(h) Let Q = P − 400.
i. Explain why Q is an exponential function .
ii. What does dQ/dt equal? Hint: it’s a multiple of Q .
3. A local band has made a music CD which they are
selling. The manager has told you that
they make the same profit for each CD sold. The profit is the revenue from CD
sales minus
the fixed costs for the studio and equipment rental. The manager has carefully
calculated
the amount of profit for various numbers of CD sold:
| Numbers of CDs sold |
600 |
900 |
| Profit |
$841 |
$5191 |
(a) Explain why the profit is a linear function of the
number of CDs sold.
(b) Calculate the slope of the linear function of Part (a).
(c) What is the meaning of the slope in terms of CD sales?
(d) Calculate the vertical intercept of the linear function of Part (a).
(e) What is the meaning of the vertical intercept in terms of CD sales?
(f) Calculate the horizontal intercept of the linear function of Part (a).
(g) What is the meaning of the horizontal intercept in terms of CD sales?
(h) Suppose your estimates for possible sales indicate that you will only sell
400 CDs.
How much should you charge to ensure that your fixed costs will be covered by
your
CD sales?
4. The following table shows U.S. population from census
data:
| Year |
1800 |
1810 |
1820 |
1830 |
1840 |
| Population (in millions) |
5.31 |
7.24 |
9.64 |
12.87 |
17.07 |
(a) On this paper plot the logarithm of the population as
a function of t, years since
1800.
(b) What property of the plot from (a) allows you to conclude that the original
data is
exponential?
(c) Find an exponential function which best approximates the population as a
function
of t.
(d) What is the annual percentage growth rate of the population?
(e) What is the decade percentage growth rate of the population?
(f) Estimate the population in 1870. The actual figure was about 39 million.
What
could explain the difference between your exponential model prediction and the
actual
figure?
(g) The decade growth rate from 1930 to 1940 was 7.2%. Is that very high, high,
about
right, low, or very low in comparison with what you ’d expect based on the data
from
1800 to 1840?
5. A jug of water is being drained by holding a spigot
open. Here is depth of water W in
inches at various t, minutes that the spigot has been open:
| Time open t |
0 |
1 |
2 |
3 |
| Water depth W |
15.50 |
11.71 |
8.45 |
5.72 |
(a) Show that W can be modeled as a quadratic function of
t.
(b) Write a formula for W as a quadratic function of t.
(c) How long will it take for the jug to be completely drained?
(d) Is W increasing or decreasing?
(e) Is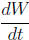 
positive or negative ?
(f) Explain why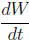 
is linear.
(g) Carefully make three graphs:
i. Graph W as a function of t for t from zero until the jug is drained.
ii. Sketch a graph of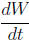 
as a function of t for
the same interval.
iii. Sketch a graph of the rate of chang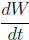e of 
,
that is, the second order rate of
change of W, as a function of t for the same interval.
6. For each of the following data tables determine whether
the data is linear, quadratic,
exponential, or power and give the appropriate formula. For credit you must
explain your
work.
Table A
Table B
| x |
1 |
2 |
3 |
4 |
| y |
2.000 |
2.297 |
2.492 |
2.639 |
Table C
| x |
0 |
1 |
2 |
3 |
| y |
2.000 |
1.740 |
1.514 |
1.317 |
