We begin our serious look at functions with linear functions , whose graphs are
lines. Lines
are ubiquitous in calculus: in fact, differential calculus is primarily focused
in using lines (linear
functions) to approximate curves (nonlinear functions). Consequently, they
warrant some special
attention:
Definition: A vertical line is a set of all points satisfying the
equation x = c for some fixed
c. Let f(x) = mx + b be a linear function . We call the graph of f a
(non-vertical) line in the
plane. We call m the slope of the line , and b the y-intercept.
Example: Given two points in the plane P1(x1; y1) and P2(x2, y2), find an
equation of the
line that passes through both.
Solution : If x1 = x2, then the vertical line x = x1 passes through them both, so
we suppose
x1 ≠ x2. Then the line is the graph of f(x) = mx + b for some m,b,
so we need to find m and
b with the conditions that f(x1) = y1 and f(x2) = y2 (so that P1 and P2 are in
the graph of f).
That gives us two linear equations,
mx1 + b = y1, and mx2 + b = y2
in two unknowns (m, b). From the first equation, we get b = y1 - mx1, and
substituting this into
the second equation, we get
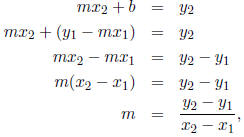
and since there is no m or b on the right-hand side, we have a definite value
for m . Using our
equation for b in terms of m, we see that
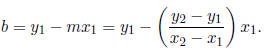
Therefore
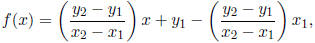
and since our line is the graph, its equation is therefore y = f(x), or
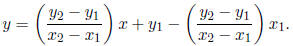
From the example, we get two very important formulas: first, that the slope
of a line through
any two points P1(x1, y1) and P2(x2, y2) with x1
≠ x2 is
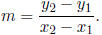
The slope is a measurement of the steepness that a function increases or
decreases, which can be
seen in the angles the graphed lines make with the x-axis. Moreover, we see that
the slope of a
vertical line would be undefined, since we would have to divide by 0.
The second formula we ¯find is an equation for a line provided you know one point
P1(x1, y1),
and the slope:
y = mx + y1 - mx1,
or
y - y1 = m(x - x1),
the point-slope form of a line. The more standard form of writing the equation,
y = mx+b, is
called the slope- intercept form .
Example: Find the equation of a line passing through the point (1, 1) with slope
7.
Solution: We're given the slope, m = 7, and an initial point (x1, y1) = (1, 1),
so the form
of the equation to use is point-slope:
y - y0 = m(x - x0);
or
y - 1 = 7(x - 1):
Rewriting into slope intercept form by solving for y , we get
y = 7(x - 1) + 1 = 7x - 7 + 1 = 7x - 6;
so the line we want is y = 7x - 6:
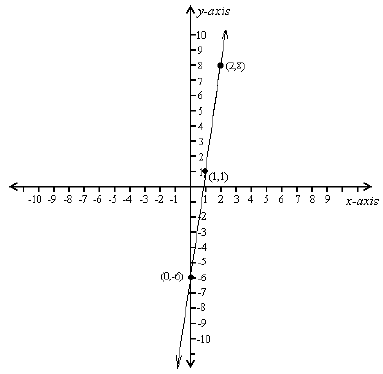
Sketch of y = 7x - 6.
As was mentioned earlier, functions give us a slightly more general way of
looking at equations:
De¯nition: We de¯ne the graph of an equation in x and y to be the set of all
points
(a, b) that satisfy the equation when a is substituted for x and b is
substituted for y. From this
de¯nition, we see that the graph of a function f(x) is really the graph of the
equation y = f(x).
So, when we say the graph of f(x) = mx + b, we also mean the graph of the
equation
y = mx + b. The two notations (f(x) and y) will be used interchangeably.
Definition: We say two (non-vertical) lines are parallel if they have the same
slope. We
say two lines are perpendicular if their slopes are negative reciprocals , i.e.
the product of their
slopes is -1.
Example: The lines y = x and y = x + 3 are parallel: both have slope 1.
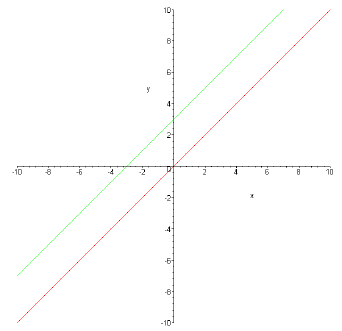
Sketch of y = x and y = x + 3.
Example: The lines 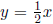 and y = -2x are
perpendicular: the slope of
and y = -2x are
perpendicular: the slope of 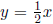 is
is
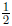 , the
, the
slope of y = -2x is -2, and 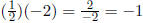 .
.
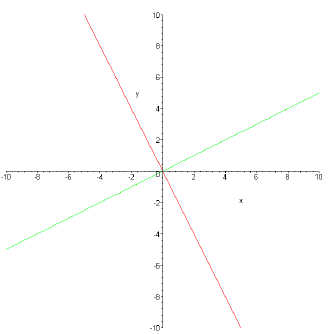
Sketch of y = (1/2)x and y = -2x.
Let's look now at taking a function whose graph we know, say y = f(x), and
determining
what function g(x) gives us the same shape, but shifted up/down and left/right.



