Section 2.4 - Matrices
• The size of a matrix is always number of rows × number of columns.
• cijrepresents the entry of the matrix C in row i and column j.
• To add and subtract matrices, they must be the same size.
• When adding or subtracting matrices , add or subtract corresponding entries.
• A scalar product is computed by multiplying each entry of a matrix by a scalar
(a number).
• Transpose - The rows of the matrix A become the columns of AT .
Section 2.5 - Multiplication of Matrices
• The matrix product AB can be computed only if the number of columns of A
equals the number of rows of B.
• If C = AB, then cij is computed by multiplying the ith
row of A by the jth
column of B.
• Identity Matrix - Denoted by In, the identity matrix is the n×n
matrix with 1’s down the main diagonal (from upper
left corner to lower right corner) and 0’s for all other entries.
• If A is m×n, then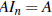 
and
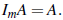
Section 2.6 - The Inverse of a Square Matrix
• Only square matrices can have inverses, but not all square matrices have
inverses.
• A square matrix that does not have an inverse is called a singular matrix.
• The inverse of A, denoted A-1, is the square n×n matrix such that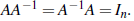 
• Systems of equations can be represented as a matrix equation of the form AX =
B where A is the coefficient matrix ,
X is a column vector containing the variables , and B is a column vector
containing constants.
• If A has an inverse, the solution to the matrix equation is X = A-1B.
• If A does not have an inverse (i.e., if A is singular), this does NOT imply
the system has no solution. It simply
means that you must use another method to solve the system.
Section 2.7 - Leontief Input-Output Model
• The input-output model is used to study the relationship between industrial
production and consumer demand.
• If A is the input-output matrix and X represents the total output of all
industries, then AX represents the internal
consumption for that economy.
• Subtracting the internal consumption from the total output gives the net
output of goods and services for consumer
demand, D:
X −AX = D
• To find the amount of goods and services that must be produced to satisfy
consumer demand, solve for X in the
above equation to obtain
X = (I−A)-1D
1. Let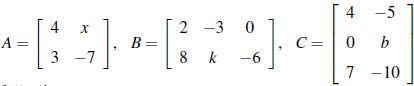
and
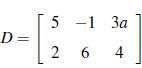.Compute each of
the following:
(a) B+3D
(b) 2C+B
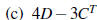
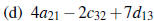
(e) DB
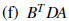
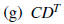
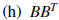
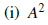
2. Using matrix algebra , solve for the matrix D:
D = AD+B
3. Solve for x and y:
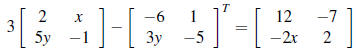
4. The times (in minutes) required for assembling,
testing, and packaging large and small capacity food processors
are shown in the following table:
| |
Assembling |
Testing |
Packaging |
Large
Small |
45
30 |
15
10 |
10
5 |
(a) Define a matrix T that summarizes the above data.
(b) Let M =[100 200] represent the number of large and small food processors
ordered , respectively. Find
MT and explain the meaning of its entries.
(c) If assembling costs $3 per minute, testing costs $1 per minute, and
packaging costs $2 per minute, find a
matrix C that, when multiplied with T, gives the total cost for making each size
of food processor.
5. If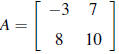 
, find A-1.
6. If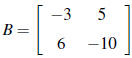 
find B-1.
7. Solve the following system of equations using matrix
inverses.
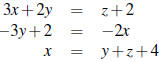
8. A small village has two major industries: steel and
electronics. For each unit of steel produced, 0.02 units of steel
and 0.15 units of electronices are used by the village. For each unit of
electronics produced, 0.1 units of steel and
0.01 units of electronics are used by the village. The remaining steel and
electronics products are then available to
export to a local city. If that city demands 500 units of steel and 800 units of
electronics, how many units of steel
and electronics pruducts should be produced by the village to meet its own needs
and those of the city?
9. Consider three sectors of the US economy: crude
petroleum (crude), petroleum-refining and related industries
(refining), and chemical production (chemical). The following table gives the
number of units of crude, refining,
and chemical products consumed in the production of one unit of crude product,
one unit of refining product, and
one unit of chemical product.
| To |
Crude |
Refining |
Chemical |
| From Crude |
0.31 |
0.42 |
0.050 |
| Refining |
0.0086 |
0.11 |
0.13 |
| Chemical |
0.010 |
0.47 |
0.38 |
(a) What is the input-output matrix for this problem?
(b) Explain the meaning of the entries in row 1 of this matrix.
(c) How many units of refining products are consumed in the production of 7,500
units of crude product?
(d) How many units of chemical products are required to produce 500 units of
each sector in this economy?
(e) If a neighboring city demands 5,500 units of crude
products, 6,750 units of refining products, and 1,250 units
of chemical products, how much should this economy produce to satisfy internal
consumption and meet the
city’s demand?
(f) Referring to (e), how many units of each product are consumed internally in
meeting the other city’s demands?
