2007-A-1. Find all values of α for which the curves y
= αx2 + αx+1/24 and x = αy2 + αy +1/24 are
tangent to each other.
2007-A-2. A repunit is a positive integer whose digits in base 10 are all
ones. Find all polynomials f
with real coefficients such that if n is a repunit, then so is f(n).
2007-B-1. Let f be a polynomial with positive integer coefficients. Prove
that if n is a positive integer,
then f(n) divides f (f(n) + 1) if and only if n = 1.
2007-B-4. Let n be a positive integer. Find the number of pairs P,Q of
polynomials with real
coefficients such that
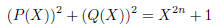
and deg P > deg Q.
2007-B-5. Let k be a positive integer. Prove that there exist polynomials
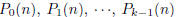
(which may depend on k) such that, for any integer n,
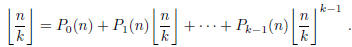
2006-B-1. Show that the curve x3 + 3xy + y3 = 1 contains
only one set of three distinct points A,B,
and C, which are the vertices of an equilateral triangle, and find its area.
2005-A-3. Let p(z) be a polynomial of degree n, all of whose zeros have absolute
value 1 in the complex
plane. Put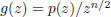 
. Show that all zeros of g '(z) = 0 have absolute
value 1.
2005-B-1. Find a nonzero polynomial P(x, y) such that
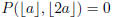for all
real numbers a . (Note:
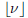is the greatest integer less than or equal to
.)
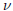2005-B-5. Let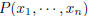 
denote a polynomial with
real coefficients in the variables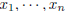 
, and
suppose that
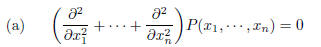(identically)
and that
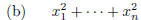divides
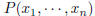
Show that P = 0 identically.
2004-A-4. Show that for any positive integer n there is an integer N such
that the product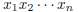 
can be expressed identically in the form
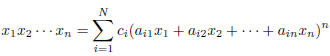
where the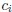 
are rational numbers and each
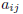is one of
the numbers, −1, 0, 1.
2004-B-1. Let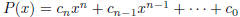 
be a
polynomial with integer coefficients. Suppose
that r is a rational number such that P(r) = 0. Show that the n numbers
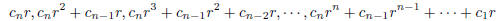
are integers.
2003-A-4. Suppose that a, b, c, A,B,C are real numbers, a ≠ 0 and A ≠ 0, such
that
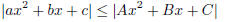
for all real numbers x. Show that
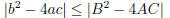
2003-B-1. Do there exist polynomials a(x), b(x), c(y),
d(y) such that
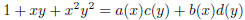
holds identically?
2003-B-4. Let
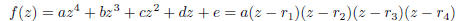
where a, b, c, d, e are integers, a ≠ 0. Show that if
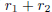is a rational number, and if
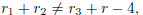
then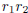 
is a rational number.
2002-A-1. Let k be a positive integer. The nth derivative of 1/(xk−1) has the
form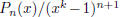 
where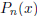 
is a polynomial. Find
.
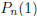2002-B-6. Let p be a prime number. Prove that the determinant of the matrix
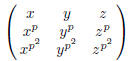
is congruent modulo p to a product of polynomials in the
form ax + by + cz, where a, b, c are integers. (We
say two integer polynomials are congruent modulo p if corresponding coefficients
are congruent modulo p.)
2001-A-3. For each integer m, consider the polynomial
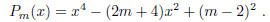
For what values of m is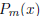 
the product of two nonconstant polynomials with integer coefficients?
2001-B-2. Find all pairs of real numbers (x, y) satisfying the system of
equations
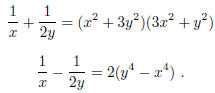
2000-A-6. Let f(x) be a polynomial with integer
coefficients. Define a sequence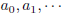 
of integers
such that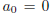 
and
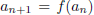for n ≥ 0. Prove that if there exists a positive
integer m for which
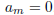, then either
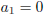or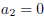 
.
1999-A-1. Find polynomials f(x), g(x) and h(x), if they
exist, such that, for all x,
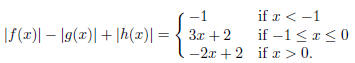
1999-A-2. Let p(x) be a polynomial that is non-negative
for all x. Prove that, for some k, there are
polynomials 
such that
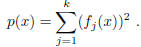
1999-B-2. Let P(x) be a polynomial of degree n such that
P(x) = Q(x)P''(x), where Q(x) is a
quadratic polynomial and P''(x) is the second derivative of P(x). Show that if
P(x) has at least two distinct
roots then it must have n distinct roots. [The roots may be either real or
complex.]
1997-B-4. Let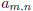 
denote the coefficient of xn in the expansion of (1 + x +
x2)m. Prove that for all
k ≥ 0,
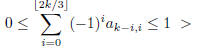
1995-B-4. Evaluate
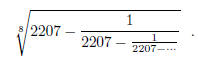
Express your answer in the form
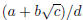, where a, b, c, d are integers.
1993-B-2. For nonnegative integers n and k, define Q(n, k) to be the coefficient
of xk in the expansion
of (1 + x + x2 + x3)n. Prove that
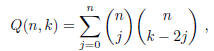
where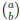 
is the standard
binomial coefficient . (Reminder: For integers a and b with a ≥ 0,
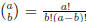
for 0 ≤ b ≤ a and 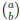= 0 otherwise.)
