Polar Form of Complex Numbers , DeMoivre's Theorem
History of Complex Numbers : Historically, complex
numbers came about when trying to solve
quadratic equations such as
x2 + 2x + 2 = 0:
In general, when trying to solve the quadratic equation ax2 + bx + c = 0, we use
the quadratic
formula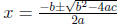 
. Applying this formula to our
quadratic equation yields the two solutions
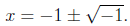
As in this example, the quadratic formula may yield
solutions involving the square root of a negative
number. As such, we introduce the "complex number system " with the properties as
the real
numbers with the added property that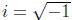 
, so that
i2 = -1.
Some felt that no meaning could be given to such expressions , which were
therefore termed "imag-
inary".
Definition: Complex numbers are represented by expressions of the form
z = a + bi
where a = Rez is the real part of z and b = Imz is called the imaginary part of
z. Graphically, we
graph a complex number in the complex plane with a real axis (horizontal) and an
imaginary axis
(vertical).
Exercises: Sketch the following complex numbers in the complex plane:
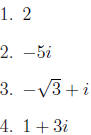
Definition: The modulus (or absolute value) of the complex
number z = a + bi is
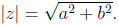
Definition: A complex number z = a + bi has polar (or
trigonometric) form
z = r(cos θ + i sin θ),
where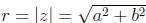 
is the modulus of z and θ is the
argument of z satisfying tan θ = b/a.
Exercises: Write each of the following complex numbers in
polar form
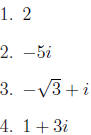
Multiplication and Division of Complex Numbers: If
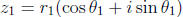and
,
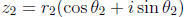then
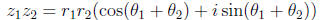
and if 
,
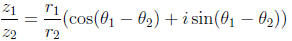
Proof: This follows immediately from the sum and difference
formulas for sine and cosine.
Exercises:
1. Write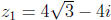 
and
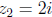in polar form and then find
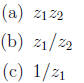
2. Write z1 = 1 - i and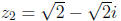 
in polar form and then find
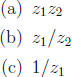
3. Let z = r(cos θ + i sin θ). Find formulas for
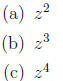
DeMoivre's Theorem: If z = r(cos θ + i sin θ) and n is any
positive integer, then
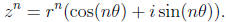
Exercise: With =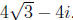 
,
find
z3.
nth Roots of a Complex Number: Reversing DeMoivre's Theorem will allow us to
find
the
n-roots of a complex number . That is, given z = a + bi, find w such that wn = z.
To do so, we
write
z = r(cos θ + i sin θ)
so that one such w is
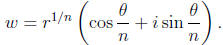
Replacing θ with θ + 2kπ for k = 0,... , n - 1 give all
of the distinct nth roots of z. That is, the n
distinct nth roots of z = r(cos θ + i sin θ) are given by
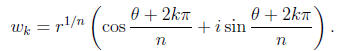
Exercises:
1. Find the cube roots of i
2. Find the 6th roots of 1.
