Tomorrow: Questions and answers, on chapters 1–3,
and the current home works.
Wednesday: Exam 1, closed books and notes, no calculators. I won’t be
able to answer
questions during the exam, on your way out pick up an answer sheet. Do check
your
answers.
Understand every term , phrase, and concept mentioned in
the following notes.
Go over them today, and ask any questions tomorrow. Everything you see here
is covered in the textbook.
• Base conversion. To convert from base 10 to another
base, use repeated division with
remainder . To convert to base 10 from another base, use nested multiplication.
Indicate a
base other than 10 by writing the word describing the base as a subscript.
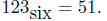
• Sets and Venn Diagrams. Understand the following
notations:
x ∈ A, A∩B, A∪B, A−B, A ⊆ B, n(A), {a, b, c} , {x|something about x} .
Know how to draw and use Venn diagrams.
• Vocabulary of arithmetic operations . add, multiply,
subtract, divide, addition, multiplication,
division, subtraction, sum, product, difference, quotient, term, addend,
minuend,
subtrahend, divisor, dividend, plus, minus, times , divided by, +, −, /, ×,
*, a
missing
operator means multiplication. Precedence of operations: multiplication and
division
come before addition and subtraction , for operations of equal precedence work
from left to
right, use parentheses to overrule these conventions. Powers, exponent, base, ˆ
, **. Concepts
of >, <, ≥, ≤, =, ≠. Whole Number Line . Thousands, millions, billions,
trillions,
quadrillions, quintillions.
• Properties of arithmetic operations with whole numbers.
Associative, Commutative, Closure,
Identity properties of addition and multiplication, Distributive Law . Rules for
powers .
Anything non-zero to the power zero is 1. Zero to any positive power is zero. 1
to any
power is 1. You multiply two powers with the same base by adding the exponents,
and
you take a power to a power by multiplying the exponents. Division by zero, and
zero to
the power zero are undefined.
• Roman Numbers . Be able to convert back and forth between
Roman and decimal numbers .
Understand the conventions (add if the smaller is to the right, subtract if it ’s
to the left)
and know the meaning of the symbols : I, V, X, L, C, D, M.
• Word problems. Go over past word problems. Many of the
problems in hw 1 (and later
hws) come with solutions .
Understand the techniques we discussed of introducing the
arithmetic operations. Addi-
tion: Set and measurement models; Subtraction: set model (the textbook calls
this the
“take away approach”), the missing addend approach; Multiplication: repeated
addition,
set model ( Cartesian product ), rectangular array (measurement) approach;
Division: parti-
tive and measurement division, missing factor approach. Powers: repeated
multiplication.