These two pages are a very brief summary of some of the
topics from basic mathematics that you should
already be familiar with from your prerequisite math and programming courses.
Working knowledge of these
topics will serve you well in this class. Don’t just memorize these facts; be
prepared to apply them.
1 Associative, Commutative, and Distributive Laws
• Associativity: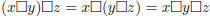 
, where 
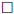can be addition or
multiplication over integers.
• Commutativity: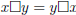 
, where 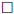can be addition or
multiplication over integers.
• Distributivity: Given operators 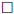and
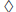over a set S, we say that 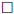is distributive
over 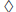if
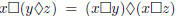and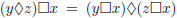 
.
(That is, 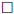is both left–distributive and
right–distributive over .)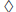
2 Fractions
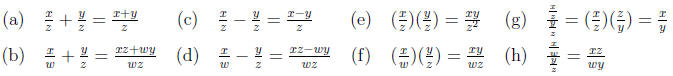
3 The Modulo Operator
• Commonly , the modulo operator (%) gives the remainder of an integer division.
• More generally: Values b and r are said to be congruent modulo m (written b ≡
r(modm)) if the result
of (b − r)/m is an integer. b is called the base, r is the residue or remainder,
and m is the modulus.
• A related operator: We say that x divides y (written x | y) if y%x = 0.
4 Exponents and Logarithms
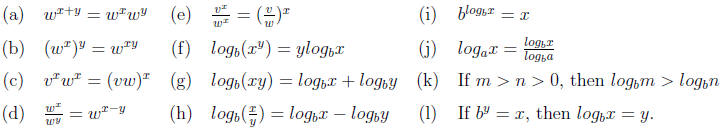
5 Factoring Quadratics
A quadratic polynomial has the form ax2 + bx + c, where a, b, and c are numbers
(usually integers).
When a = 1 : (x + d)(x + e) = x2 + (d + e)x + de
When a ≠ 1 : (fx + d)(gx + e) = (fg)x2 + (dg + fe)x + de
6 The Quadratic Formula
We use the quadratic formula to find a solution to a quadratic equation , not to
factor the corresponding
quadratic polynomial.
Assuming that a ≠ 0, the solutions (a.k.a. x-intercepts, a.k.a. roots ) of ax2 +
bx + c = 0 are:
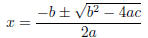
7 Laws of Inequalities
• a ≤ b is true when a < b or a = b. Similarly for ≥ and >.
• For any c: if a < b, then a + c < b + c. Similarly for ≤, >, and ≥.
• For any positive c: if a < b. then ac < bc. Similarly for ≤, >, and ≥.
• For any negative c: if a < b. then ac > bc. Similarly for ≤, >, and ≥.
• In the following, you can replace < with > so long as you also replace ≤ with
≥:
If a < b and b < c, then a < c If a ≤ b and b < c, then a < c
If a < b and b ≤ c, then a < c If a ≤ b and b ≤ c, then a ≤ c
8 Summation and Product Notation
• Summation: In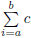 
,∑ is the Greek letter
(capital) sigma; i is the index of summation, or just index ; a
is the lower limit ; b is the upper limit ; and c is the sequence, usually in
terms of the index .
• Product: In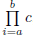 
, the nomenclature is the same,
except that the symbol is the capital letter pi
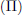and
the index is called the index of multiplication.
9 Number Systems
• Binary: Base 2, Digits 0,1
• Octal: Base 8, Digits 0-7
• Decimal : Base 10, Digits 0-9
• Hexadecimal: Base 16, Digits 0-9 and A-F
