Matrices

• The dimension of a matrix is the number of rows by the number of columns. i.e. The dimension
of matrix A is 3 x 4. It has 3 rows and 4 columns.

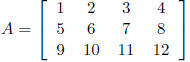
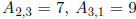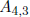We can reference individual elements of a matrix by using subscripts: and is
not defined.

• A square matrix has an equal number of rows and columns.

• An identity matrix is a square matrix that is all zeros except the main diagonal which is all ones.
See page 128 for an example.

• Two matrices are equal provided they have the same dimension and the corresponding entries are
equal. i.e.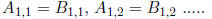

• Entering a matrix into the calculator. On the TI-83 press MATRX or if you have a TI-83 Plus
press to get to the matrix window. Now press twice to get to edit mode. Use and
to select a matrix to edit and then press . As you enter the values, press or to
go to the next entry of the matrix. When you are finished entering the matrix press . This
will quit the matrix screen.

Note: All matrix operations may be done with the calculator as long as the matrix does not contain
a variable in it . As soon as there is a letter in the matrix, then you must do the operation by hand.

• Matrix operations.

- Scalar multiplication: This is just multiplying a matrix by a number. For example 3A means
that you multiply every entry in matrix A by the number 3.
- Addition/subtraction: The matrices must be the same dimension for this to work. You just
add/subtract corresponding enteries.
- Multiplication: Matrix multiplication is not like normal multiplication. It is very dependent
on the order that the matrices are multiplied. To multiply AB, then the number of columns of
matrix A must be equal to the number of rows of matrix B. See pages 126-128 for an example.
- Division : There is no division operation for matrices.
- Inverses: Square matrices are the only matrices that might have an inverse; however, not all
square matrices will have an inverse. The notation of the inverse of an matrix is B^-1. If the
matrix B is listed below and it has been entered into the calculator in matrix B (see above)
then we can try to compute the inverse by first getting to the matrix window and then pressing
. We would get the answer on the right.

If an inverse doesn't exist, then the calculator will respond SINGULAR MAT

A systems of equations can be written in as a matrix equation, AX = B where A is the coefficient
matrix, X is the variable matrix, and B is the constants matrix. See example 7 page 130.

Section 2.2 and 2.3 Gauss-Jordan Method

An augmented matrix is made by joining the coefficient matrix with the constant matrix. It
represents a system of equations in a single matrix. See pages 84-85.

•An augmented matrix is transformed to Row- Reduced Form (or Reduced Row Echelon Form) by the
Gauss- Jordan method . We do this so that we can read o the answer to the system of equations.

An augmented matrix is in Reduced Row Echelon Form provided:

- The first non zero number in a row is a one. Called a leading one.
- The leading one is the only nonzero entry in its column.
- The leading ones are positioned in a diagonal- like manner starting at the upper left going to the
lower right. (i.e. A row with fewer zeros before a leading one is above a row with more zeros
before the leading one.)

• These are the Gauss-Jordan row operations used to manipulate a matrix into Reduced Row Echelon
Form.

- Swap rows.
- Multiply a row by a nonzero constant.
- Add a multiple of one row to another row.

For examples of the row operations performed look at examples 5, 6, and 7 in section 2.2. You should
know how to perform given row operations. i.e. problems 27-30 in section 2.2.

• Reading o the solution of an augment matrix in Reduced Row Echelon Form.

- If there is a row that is all zeros except the last number and it is nonzero then this means that
there is no solution to the system of equations.

- If the number of leading ones is equal to the number of variables that means there is a single
solution to the system of equations. i.e. has a single solution and the solution
is x = 3, y = 5, and z = 9.

- If the number of leading ones is less than the number of variables (and you are not in the no
solution case) then there is an infinite number of solutions to the system of equations. The
solution is found by writing the equations given by the matrix in rref form and solving for those
variables that have a leading one in their columns. i.e. The solution to 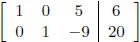is
and z = any number. z is called the parameter for this problem. (Actually
any variable that does not have a leading one in its column is a parameter.) To get a particular
solution, just plug in a value for the parameter .

• The calculator can take an augmented matrix to Reduced Row Echelon Form in one step. Enter the
augmented matrix into the calculator, say matrix A. Now go to the matrix window and press .
Go down the list until you find rref( and select this command. Go back to the matrix window and
select the matrix that you want put into Reduced Row Echelon Form. On the screen you should now
see
rref([A]
Now press and the hard work is done.
Note: This only works if the number of columns in the augmented matrix is greater than or equal to
the number of rows. If you matrix doesn't meet these requirements, then you must do Gauss-Jordan
by hand or find some other method. All of these matrices(on the next page) can not be solved by the
rref command on the TI-83 as they are written.