p 83, #16. In order to find a chain
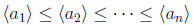
of subgroups of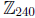 
with n as large as possible, we start at the top with
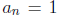so that
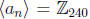. In general, given
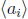we will choose
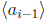to be the largest
proper subgroup
of 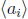. We will make repeated use of the fundamental theorem of cyclic groups
which tells
us that a cyclic group of order m has a unique subgroup of order d for any d | m.
The largest proper subgroup of 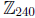has size 120 and is
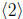. Since |2| = 120,
the largest
proper subgroup of 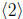has size 60 and is
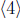. Since |4| = 60, the largest
proper subgroup of
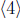has size 30 and is
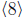. Since |8| = 30, the largest proper subgroup of
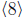has order 15
and is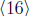 
. Since |16| = 15, the largest possible subgroup of
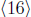has order 5 and is
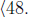
Finally, since |48| = 5 is prime, the only proper subgroup of
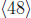is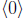 
.
Therefore, we have
produced the maximal chain
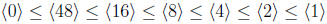
which has length 7. Notice that the chain
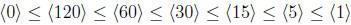
also has length 7, but is produced in the opposite way, i.e. by starting with
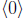and at each
stage choosing
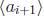as the smallest subgroup containing
.
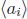p 83, # 20. Let x ∈ G. Since x35 = e, we know that |x| = 1, 5, 7 or 35.
Since |G| = 35,
if G contains an element x of order 35, then G =
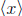as desired. On the other
hand, if G
contains an element x of order 5 and and element y of order 7, then, since G is
abelian
(xy)35 = x35y35 = ee = e
so that the order k of xy divides 35. That is, |xy| = 5, 7 or 35. If |xy| = 5
then
e = (xy)5 = x5y5 = ey5 = y5
which means that 7 = |y| divides 5, a contradiction. Likewise , we have a similar
problem if
|xy| = 7. It follows that |xy| = 35, and as above that G is cyclic.
So, what we need to do is show that G must have an element of order 5 and an
element of
order 7. We argue by contradiction. If G has no elements of order 5 then every
non-identity
element of G has order 7. That is, there are 34 elements in G or order 7.
However, by the
corollary to Theorem 4.4, the number of elements in G of order 7 is divisible by
Ø(7) = 6,
and 34 is not divisible by 6. Likewise, if G had no element of order 7 then G
would contain
34 elements of order 5, and this number would have to be divisible by Ø (5) = 4,
which is
also impossible. It follows that G must have at least one element of order 5 and
at least one
of order 7. As we pointed out above, this forces G to be cyclic.
This argument does not work if 35 is replaced by 33, because 33 = 3·11 and Ø(3) =
2 does
divide 32 = 33 − 1, and so we cannot eliminate the case that G consists only of
elements of
orders 1 or 3. Nevertheless, we will see later that every abelian group of order
33 is, indeed,
cyclic.
p 84, # 36. (=>)) Suppose that G is the union of the proper subgroups
Hi, for i ∈ I (I is
some indexing set). Let a ∈ G. Then there is an i ∈ I so that a ∈ Hi, and by
closure we
have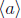 
≤ Hi. Since Hi ≠ G, it must be the case that
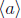≠ G. Since a ∈ G was
arbitrary,
we conclude that G cannot be cyclic.
(
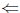) Now suppose that G is not cyclic. For any a
∈ G we know that (1) a ∈ 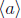and
(2)
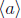≠ G. It follows that
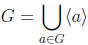
expresses G as the union of proper subgroups.
p 84, # 40. The proof of the fundamental theorem of cyclic groups shows
that if 0 ≠ H ≤ Z
then H = 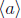where a is the least positive
integer in H. Since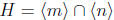 
consists of all
the integers that are common multiples of m and n , it must be the case that H =
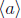where
a is the least common multiple of m and n. That is
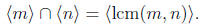
p 85, # 56. It is enough to show that U(2n) has two distinct elements of order
2, say a
and b. For then U(2n) will have the non-cyclic subgroup {1, a, b, ab}.
Let a = 2n − 1 and b = 2n-1 − 1. Since n ≥3, we see that a, b ≠ 1. So to show
that a
and b have order 2 in U(2n) we need only show that a2 mod 2n = b2 mod 2n = 1.
Well
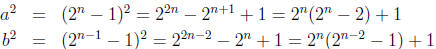
which give the desired conclusion since n > 2.
p 85, # 60.
Proposition 1. Let |x| = n. Then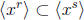 
if
and only if (n, s)|(n, r)
Proof. (=>) Suppose that 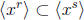. Then |xr| divides |xs|.
Since |xr| = n/(n, r) and
|xs| = n/(n, s), this means there is a k so that kn/(n, r) = n/(n, s). That is,
k(n, s) = (n, r),
which is what we sought to show.
() Now suppose that (n, s)|(n, r). Then, as above, we can show that n/(n, r)|n/(n,
s).
Since |xs| = n/(n, s), the fundamental theorem of cyclic groups implies that
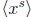has a
unique subgroup, H, of order n/(n, r). But n/(n, r) also divides n = |x|, so
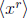is the
unique subgroup of 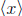of order n/(n, r). Since H is a subgroup of
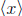with this
property , it
must be the case that
.
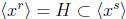p 85, # 64. Let x ∈ Z(G), x ≠ e. By hypothesis, |x| = p, a prime. Let y∈ G, y ≠
e, x -1.
Then |y| = q and |xy| = l, both primes. Since x ∈ Z(G) we see that
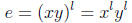
so that
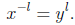
But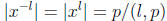 
and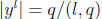 
and so
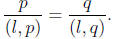
or
p(l, q) = q(l, p).
Since l, p, q are prime, this is only possible if p = q = l. That is, for any y
∈G, |y| = p = |x|.
