1. Study the questions from Exams #1-#5.
2. Graph the following: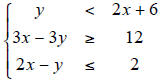 
3. Write sec θ in terms of sin θ where θ is in
quadrant II.
4. For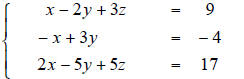 
a) Use the Elimination Method to solve
the above system.
5. For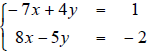 
a) Convert the above system to a matrix
equation.
b) Find the inverse of the coefficient
matrix.
c) Use the result of part b) to find to
solve the system.
6. A biologist has two alcohol solutions, one
solution containing 5% methane and the
other containing 20% methane. How many
milliliter of each solution should he mix to
produce 1L of a solution that contains 14%
methane? For practice use the Matrix
Method and the inverse of the matrix.
7. Two straight roads diverge at an angle of
75°. Two cars leave the intersection at 2:00
P.M., one traveling at 55 mph and the other
at 30 mph. How far apart are the cars at
3:30 PM?
8. For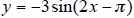 
,
a) Find the amplitude
b) Find the period
c) Find the phase shift of the function
d) Sketch the graph
9. Solve the logarithmic equation for x :
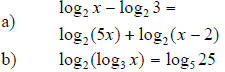
10. Let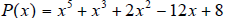 
a) List all of the possible rational roots .
b) Use the Descartes’ rule of signs to
determine the possible number of
positive and negative real zeros.
c) Find the upper and the lower bound
d) Without actually factoring,
determine how many positive real
zeros, negative real zeros , and
imaginary zeros we could have.
e) Using the synthetic division and the
information above to find all of the
roots including the real and complex
roots.
11. Let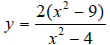 
a) Find the x- intercept .
b) Find the y-intercept.
c) Find the asymptotes.
d) Use the above information to graph.
12. Find a fourth-degree polynomial with
integer coefficients that has zeros 2i and -2
with -2 a zero of multiplicity 3.
13. Factor the following expressions
completely:
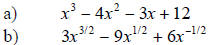
14. Solve each inequality . Sketch the solution
on a real number line, and write the solution
using the interval notation:
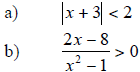
15. A ball is thrown straight upward at an initial
speed of 40 ft/s. How high is the highest
point the ball reaches? Use the formula
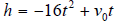discussed in the lecture and
the discriminant of the quadratic formula.
16. Use the property of Inverse Functions to
find the range and domain of the
following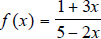 
. What two
assumptions do we have to find the inverse
function?
17. Find the expansion of
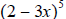
a) Using the Pascal’s triangle.
b) Using the Binomial Theorem .
18. Find the sum of 1+3+9+…+2187
19. The common ratio in a geometric sequence
is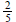 
, and the fourth term is
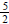. Find the
fifteenth term.
20. Write the sum using sigma notation
for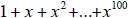 
.
21. Graph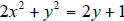 
22. Convert the polar equation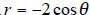 
to
the rectangular coordinates .
23. Find parametric equations for the line of
slope 3 that passes through the point (2, 6).
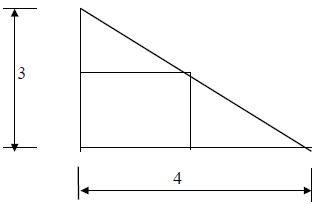
24. Find the area of the largest rectangle that can
be inscribed in a right triangle with legs 3
cm and 4 cm if two sides of the rectangle lie
along the legs as show below.
